
【題目】如圖,O是等邊三角形的旋轉中心,∠EOF=120°,∠EOF繞點O進行旋轉,在旋轉過程中,OE與OF與△ABC的邊構成的圖形的面積( )

A. 等于△ABC面積的![]() B. 等于△ABC面積的
B. 等于△ABC面積的![]()
C. 等于△ABC面積的![]() D. 不能確定
D. 不能確定
科目:初中數學 來源: 題型:
【題目】列方程解下列實際問題
某校為美化校園,計劃對面積為1800![]() 的區域進行綠化,安排甲、乙兩個工程隊完成.已知甲隊每天完成綠化的面積是乙隊每天完成綠化面積的2倍,并且在獨立完成面積為400
的區域進行綠化,安排甲、乙兩個工程隊完成.已知甲隊每天完成綠化的面積是乙隊每天完成綠化面積的2倍,并且在獨立完成面積為400![]() 區域的綠化時,甲隊比乙隊少用4天.求甲、乙兩工程隊每天能完成綠化的面積分別是多少?
區域的綠化時,甲隊比乙隊少用4天.求甲、乙兩工程隊每天能完成綠化的面積分別是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中, ∠C=90°,邊AB的垂直平分線交AB、AC分別于點D,點E,連結BE.

(1)若∠A=40°,求∠CBE的度數.
(2)若AB=10,BC=6,求△BCE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系中的位置如圖所示.A、B、C三點在格點上.
(1)作出△ABC關于y軸對稱的△A1B1C1,并寫出點C1的坐標 ;
(2)在(1)的條件下,連接CC1交AB于點D,請標出點D,并直接寫出CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC與△A′B′C′成中心對稱,下列說法不正確的是( )

A. S△ABC=S△A′B′C′ B. AB=A′B′,AC=A′C′,BC=B′C′
C. AB∥A′B′,AC∥A′C′,BC∥B′C′ D. S△ACO=S△A′B′O
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的頂點P是BC的中點,兩邊PE、PF分別交AB、AC于點E、F,給出以下五個結論:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤![]() .當∠EPF在△ABC內繞頂點P旋轉時(點E不與點A、B重合),上述結論中始終正確的序號有 .
.當∠EPF在△ABC內繞頂點P旋轉時(點E不與點A、B重合),上述結論中始終正確的序號有 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算、化簡
(1)y2·y3·y4
(2)(-4a2b)3
(3) (22)4×(![]() )8
)8
(4)-8-(-15)+(-9)-(-12);
(5)![]() ;
;
(6)[-22-(![]() )×36]÷5;
)×36]÷5;
(7)(-1)2017-![]() ];
];
(8)5(3a2b-ab2)-4(-ab2+3a2b);
(9)(2x2y+2xy2)-[2(x2y-1)+3xy2+2].
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菜農李偉種植的某蔬菜計劃以每千克![]() 元的單價對外批發銷售,由于部分菜農盲目擴大種植,造成該蔬菜滯銷.李偉為了加快銷售,減少損失,對價格經過兩次下調后,以每千克
元的單價對外批發銷售,由于部分菜農盲目擴大種植,造成該蔬菜滯銷.李偉為了加快銷售,減少損失,對價格經過兩次下調后,以每千克![]() 元的單價對外批發銷售.
元的單價對外批發銷售.
![]() 求平均每次下調的百分率;
求平均每次下調的百分率;
![]() 小華準備到李偉處購買
小華準備到李偉處購買![]() 噸該蔬菜,因數量多,李偉決定再給予兩種優惠方案以供選擇:
噸該蔬菜,因數量多,李偉決定再給予兩種優惠方案以供選擇:
方案一:打九折銷售;
方案二:不打折,每噸優惠現金![]() 元.
元.
試問小華選擇哪種方案更優惠,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“8字”的性質及應用:
(1)如圖1,AD、BC相交于點O,得到一個“8字”ABCD,求證:∠A+∠B=∠C+∠D.
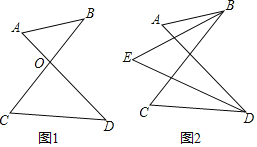
(2)如圖2,∠ABC和∠ADC的平分線相交于點E,利用(1)中的結論證明:∠E=![]() (∠A+∠C).
(∠A+∠C).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com