
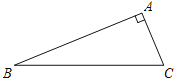
【題目】在Rt△ABC中,∠A=90°,∠B=22.5°,點P為線段BC上一動點,當點P運動到某一位置時,它到點A,B的距離都等于a,到點P的距離等于a的所有點組成的圖形為W,點D為線段BC延長線上一點,且點D到點A的距離也等于a.
(1)求直線DA與圖形W的公共點的個數;
(2)過點A作AE⊥BD交圖形W于點E,EP的延長線交AB于點F,當a=2時,求線段EF的長.
【答案】(1)1個;(2)![]()
【解析】
(1)連接AP,根據圓周角定理得到∠APD=45°,求得DA=AP=a,得到∠D=∠APD=45°,推出D A⊥PA,于是得到結論;
(2)根據等腰三角形的性質得到∠BAP=∠B=22.5°,求得∠PAC=∠PCA=67.5°,推出點C在⊙P上,根據垂徑定理得到AC=CE,求得∠APE=90°,于是得到結論.
解:(1)直線DA與圖形W的公共點的個數為1個;
∵點P到點A,B的距離都等于a,
∴點P為AB的中垂線與BC的交點,
∵到點P的距離等于a的所有點組成圖形W,
∴圖形W是以點P為圓心,a為半徑的圓,
根據題意補全圖形如圖所示,
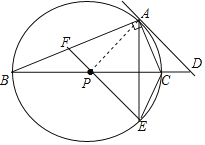
連接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵點D到點A的距離也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA為⊙P的切線,
∴直線DA與圖形W的公共點的個數為1個;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴點C在⊙P上,
∵AE⊥BD交圖形W于點E,
∴![]()
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=![]() ,∠E=45°,
,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=x2﹣2mx+m2+m的頂點為A.
(1)當m=1時,直接寫出拋物線的對稱軸;
(2)若點A在第一象限,且OA=![]() ,求拋物線的解析式;
,求拋物線的解析式;
(3)已知點B(m﹣![]() ,m+1),C(2,2).若拋物線與線段BC有公共點,結合函數圖象,直接寫出m的取值范圍.
,m+1),C(2,2).若拋物線與線段BC有公共點,結合函數圖象,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
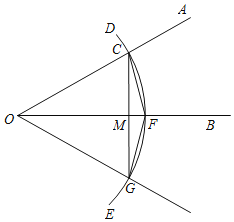
【題目】已知銳角∠AOB如圖,
(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作弧DE,交射線OB于點F,連接CF;
(2)以點F為圓心,CF長為半徑作弧,交弧DE于點G;
(3)連接FG,CG.作射線OG.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
A.∠BOG=∠AOBB.若CG=OC,則∠AOB=30°
C.OF垂直平分CGD.CG=2FG
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經過舉國上下抗擊新型冠狀病毒的斗爭,疫情得到了有效控制,國內各大企業在2月9日后紛紛進入復工狀態.為了了解全國企業整體的復工情況,我們查找了截止到2020年3月1日全國部分省份的復工率,并對數據進行整理、描述和分析.下面給出了一些信息:

a.截止3月1日20時,全國已有11個省份工業企業復工率在90%以上,主要位于東南沿海地區,位居前三的分別是貴州(100%)、浙江(99.8%)、江蘇(99%).
b.各省份復工率數據的頻數分布直方圖如圖1(數據分成6組,分別是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如圖2,在b的基礎上,畫出扇形統計圖:
d.截止到2020年3月1日各省份的復工率在80<x≤90這一組的數據是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的復工率的平均數、中位數、眾數如下:
日期 | 平均數 | 中位數 | 眾數 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
請解答以下問題:
(1)依據題意,補全頻數分布直方圖;
(2)扇形統計圖中50<x≤60這組的圓心角度數是 度(精確到0.1).
(3)中位數m的值是 .
(4)根據以上統計圖表簡述國內企業截止3月1日的復工率分布特征.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在⊙O中按如下步驟作圖:
(1)作⊙O的直徑AD;
(2)以點D為圓心,DO長為半徑畫弧,交⊙O于B,C兩點;
(3)連接DB,DC,AB,AC,BC.
根據以上作圖過程及所作圖形,下列四個結論中錯誤的是( )
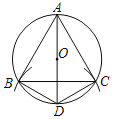
A.∠ABD=90°B.∠BAD=∠CBDC.AD⊥BCD.AC=2CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數y=kx2+(2k+1)x+1(k為實數).
(1)對于任意實數k,函數圖象一定經過點(﹣2,﹣1)和點_____;
(2)對于任意正實數k,當x>m時,y隨著x的增大而增大,寫出一個滿足題意的m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與一次函數
與一次函數![]() 的圖象交于點
的圖象交于點![]() 與反比例函數
與反比例函數![]() 的圖象交于點
的圖象交于點![]() ,點
,點![]() 與點
與點![]() 關于
關于![]() 軸對稱.
軸對稱.
(1)直接寫出點![]() 的坐標;
的坐標;
(2)求點![]() 的坐標(用含
的坐標(用含![]() 的式子表示);
的式子表示);
(3)若![]() 兩點中只有一個點在線段
兩點中只有一個點在線段![]() 上,直接寫出
上,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
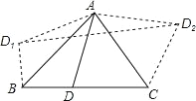
【題目】如圖,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC邊上異于點B,C的一動點,將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
+2,D是BC邊上異于點B,C的一動點,將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情無情人有情,愛心捐款傳真情.新冠肺炎疫情發生后,某班學生積極參加獻愛心活動,該班![]() 名學生的捐款統計情況如下表,關于捐款金額,下列說法錯誤的是( )
名學生的捐款統計情況如下表,關于捐款金額,下列說法錯誤的是( )
金額/元 | 10 | 20 | 30 | 50 | 100 |
人數 | 2 | 18 | 10 | 8 | 2 |
A.平均數為![]() 元B.眾數為
元B.眾數為![]() 元C.中位數為
元C.中位數為![]() 元D.極差為
元D.極差為![]() 元
元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com