
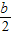 時,y=0.且b2-4c=0,即b2=4c;
時,y=0.且b2-4c=0,即b2=4c;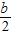 -3,n),B(-
-3,n),B(-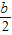 +3,n);
+3,n);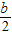 -3)2+b(-
-3)2+b(-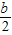 -3)+c=
-3)+c=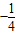 b2+c+9,所以把b2=4c代入即可求得n的值.
b2+c+9,所以把b2=4c代入即可求得n的值.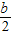 時,y=0.且b2-4c=0,即b2=4c.
時,y=0.且b2-4c=0,即b2=4c.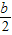 對稱,
對稱,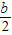 -3,n),B(-
-3,n),B(-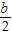 +3,n)
+3,n)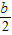 -3)2+b(-
-3)2+b(-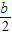 -3)+c=
-3)+c=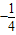 b2+c+9
b2+c+9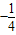 ×4c+c+9=9.
×4c+c+9=9.

 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com