

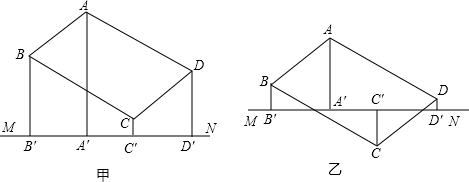
 (BB′+DD′),OO′=
(BB′+DD′),OO′= (AA′+CC′)即可;
(AA′+CC′)即可; (AA′-CC′),OO′=
(AA′-CC′),OO′= (BB′+DD′),推出AA′-CC′=BB′+DD′即可.
(BB′+DD′),推出AA′-CC′=BB′+DD′即可.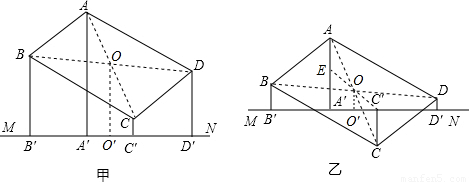
 (BB′+DD′),OO′=
(BB′+DD′),OO′= (AA′+CC′),
(AA′+CC′), A′E=
A′E= (AA′-CC′),
(AA′-CC′), (BB′+DD′),
(BB′+DD′),

 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
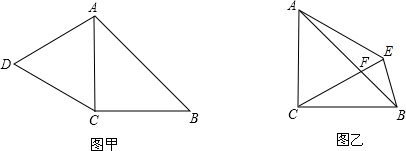
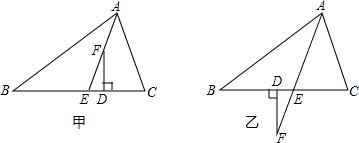 已知,如圖甲,在△ABC中,AE平分∠BAC(∠C>∠B),F為AE上一點,且FD⊥BC于D.
已知,如圖甲,在△ABC中,AE平分∠BAC(∠C>∠B),F為AE上一點,且FD⊥BC于D.| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
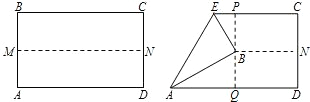
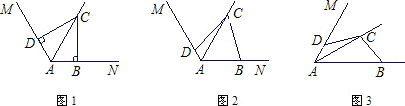
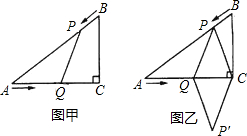
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com