【題目】如圖，(1)指出DC和AB被AC所截得的內錯角；
(2)指出AD和BC被AE所截得的同位角；
(3)指出∠4與∠7，∠2與∠6，∠ADC與∠DAB各是什么關系的角，并指出各是哪兩條直線被哪一條直線所截形成的．
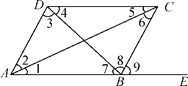
【答案】(1)∠1和∠5；(2)∠DAB和∠9；(3)∠4和∠7是內錯角，是直線DC和AB被DB所截形成的；∠2與∠6是內錯角，是直線AD和BC被AC所截形成的；∠ADC和∠DAB是同旁內角，是直線DC和AB被AD所截形成的
【解析】
（1）根據內錯角就是：兩個角都在截線的兩側，又分別處在被截的兩條直線中間位置的位置的角，可得答案；
（2）根據同位角就是：兩個角都在截線的同旁，又分別處在被截的兩條直線同側的位置的角，可得答案；
（3）根據同旁內角就是：兩個角都在截線的同旁，又分別處在被截的兩條直線中間的位置的角，根據內錯角就是：兩個角都在截線的兩側，又分別處在被截的兩條直線中間位置的位置的角，根據同位角就是：兩個角都在截線的同旁，又分別處在被截的兩條直線同側的位置的角，可得答案．
(1) DC和AB被AC所截得的內錯角是∠1和∠5；
(2) AD和BC被AE所截得的同位角是∠DAB和∠9；
(3)∠4和∠7是內錯角，是直線DC和AB被DB所截形成的；
∠2與∠6是內錯角，是直線AD和BC被AC所截形成的；
∠ADC和∠DAB是同旁內角，是直線DC和AB被AD所截形成的.
暑假作業暑假快樂練西安出版社系列答案科目：初中數學 來源： 題型：
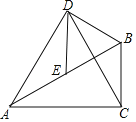
【題目】如圖，在Rt△ABC中，（M2，N2），∠BAC=30°，E為AB邊的中點，以BE為邊作等邊△BDE，連接AD，CD．
（1）求證：△ADE≌△CDB；
（2）若BC=
，在AC邊上找一點H，使得BH+EH最小，并求出這個最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
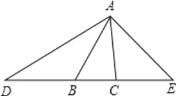
【題目】如圖，在△ABC 中，∠ABC＝50°，∠ACB＝80°，延長 CB 至 D，使 DB＝BA，延長 BC 至 E，使 CE＝CA，連接 AD 和 AE，求∠D，∠DAE 的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
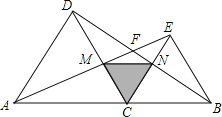
【題目】如圖，點C是線段AB上除A、B外的任意一點，分別以AC、BC為邊在線段AB的同旁作等邊三角形ACD和等邊三角形BEC，連結AE交DC于M，連結BD交CE于N，AE與BD交于F
（1）求證：AE=BD；
（2）連結MN，仔細觀察△MNC的形狀，猜想△MNC是什么三角形？說出你的猜想，并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
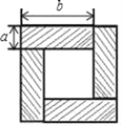
【題目】(1)如圖是用4個全等的長方形拼成的一個“回形”正方形，圖中陰影部分面積用2種方法表示可得一個等式，這個等式為_______．
(2)若(4x﹣y)2=9，(4x+y)2=169，求xy的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
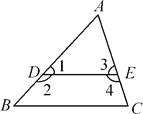
【題目】如圖，(1)∠2與∠B是什么角？若∠1＝∠B，則∠2與∠B有何數量關系？請說明理由．
(2)∠3與∠C是什么角？若∠4＋∠C＝180°，則∠3與∠C有何數量關系？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在質量檢測中，從每盒標準質量為125克的酸奶中，抽取6盒，結果如下：
編號 | 1 | 2 | 3 | 4 | 5 | 6 |
質量（克） | 126 | 127 | 124 | 126 | 123 | 125 |
差值（克） | +1 |
（1）補全表格中相關數據；
（2）請你利用差值列式計算這6盒酸奶的質量和.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算：
(1)|－2|÷(－
)＋(－5)×(－2); (2)(
－＋
)×(－24)；
(3)15÷(－
＋); (4)(－2)2－|－7|－3÷(－
)＋(－3)3×(－
)2.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明同學在學習了全等三角形的相關知識后發現，只用兩把完全相同的長方形直尺就可以作出一個角的平分線．如圖：一把直尺壓住射線OB，另一把直尺壓住射線OA并且與第一把直尺交于點P，小明說：“射線OP就是∠BOA的角平分線．”他這樣做的依據是（ ）
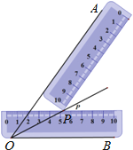
A. 角的內部到角的兩邊的距離相等的點在角的平分線上
B. 角平分線上的點到這個角兩邊的距離相等
C. 三角形三條角平分線的交點到三條邊的距離相等
D. 三角形三條垂直平分線的交點到三個定點的距離相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com