
【題目】某公司生產一種原料,運往A地和B地銷售.如表記錄的是該產品運往A地和B地供應量y1(kg)、y2(kg)與銷售價格x(元)之間的關系:
銷售價格x(元) | 100 | 150 | 200 | 300 |
運往A地y1(kg) | 300 | 250 | 200 | 100 |
運往B地y2(kg) | 450 | 350 | 250 | n |
(1)請認真分析上表中所給數據,用你所學過的函數來表示其變化規律,并驗證你的猜想,分別求出y1與x、y2與x的函數關系式;
(2)用你求出的函數關系式完成上表,直接寫出n= ;
(3)直接寫出銷售價格在 元時,該產品運往A地的供應量等于運往B地的供應量.
【答案】(1)y1=﹣x+400,y2=﹣2x+650;(2)50;(3)250
【解析】
(1)通過觀察發現,y1、y2都是x的一次函數,利用待定系數法即可解決;
(2)利用(1)的結論令![]() ,求出的
,求出的![]() 值即為n的值;
值即為n的值;
(3)根據(1)的結論,令![]() ,列方程解答即可.
,列方程解答即可.
解:(1)設y1與x的函數關系式為y1=k1x+b1,根據題意有
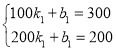 解得
解得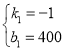
∴y1=﹣x+400,
驗證:當![]() 時,
時,![]() ; 當
; 當![]() 時,
時,![]()
設y2與x的函數關系式為y2=k2x+b2,
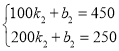 解得
解得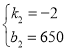
∴y2=﹣2x+650;
驗證:當![]() 時,
時,![]() ;
;
(2)當x=300時,n=y2=﹣2x+650=﹣2×300+650=50.
故答案為:50;
(3)根據題意得:﹣x+400=﹣2x+650,
解得x=250.
答:銷售價格在250元時,該產品運往A地的供應量等于運往B地的供應量.
故答案為:250.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=4,BC=6,將△ABC沿AC折疊,使點B落在點E處,CE交AD于點F,則DF的長等于( )
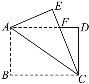
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+(m-1)x-2m2+m=0(m為實數)有兩個實數根x1、x2.
(1)當m為何值時,x1=x2.
(2)若x12+x22,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ABC=90°,AB=BC,直線l1、l2、l3分別通過A、B、C三點,且l1∥l2∥l3.若l1與l2的距離為5,l2與l3的距離為7,則Rt△ABC的面積為___________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB是⊙O的直徑,弦CD與AB相交,∠BAC=40°.
(1)如圖1,若D為弧AB的中點,求∠ABC和∠ABD的度數;
(2)如圖2,過點D作⊙O的切線,與AB的延長線交于點P,若DP∥AC,求∠OCD的度數.
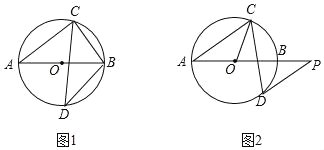
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 經過點A(
經過點A(![]() ,0),B(
,0),B(![]() ,0),且與y軸相交于點C.
,0),且與y軸相交于點C.
(1)求這條拋物線的表達式;
(2)求∠ACB的度數;
(3)設點D是所求拋物線第一象限上一點,且在對稱軸的右側,點E在線段AC上,且DE⊥AC,當△DCE與△AOC相似時,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“中華人民共和國道路交通管理條例”規定:小汽車在城街路上行駛速度不得超過![]() km/h.如圖,一輛小汽車在一條城市街路上直道行駛,某一時刻剛好行駛到路對面車速檢測儀正前方
km/h.如圖,一輛小汽車在一條城市街路上直道行駛,某一時刻剛好行駛到路對面車速檢測儀正前方![]() m處,過了2s后,測得小汽車與車速檢測儀間距離為
m處,過了2s后,測得小汽車與車速檢測儀間距離為![]() m,這輛小汽車超速了嗎?
m,這輛小汽車超速了嗎?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有長為22米的籬笆,一面利用墻(墻的最大可用長度為14米),圍成中間隔有一道籬笆的長方形花圃,有以下兩種圍法.
(1)如圖1,設花圃的寬AB為x米,面積為y米2,求y與x之間的含函數表達式,并確定x的取值范圍;
(2)如圖2,為了方便出入,在建造籬笆花圃時,在BC上用其他材料造了寬為1米的兩個小門,設花圃的寬AB為a米,面積為S米2,求S與a之間的函數表達式及S的最大值?
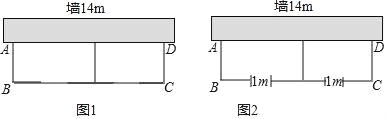
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,AB=8cm,BC=16 cm.點P從點A出發沿AB向點B以2 cm/s的速度運動,點Q從點B出發沿BC向點C以4 cm/s的速度運動.如果點P,Q分別從點A,B同時出發,則_____________秒鐘后△PBQ與△ABC相似?
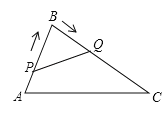
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com