
【題目】正方形ABCD的邊AB在直線MN上,O是AC、BD的交點,過O作OE⊥MN于點E.
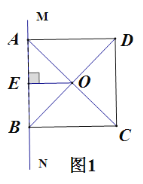
(1)如圖1,線段AB與OE之間的數量關系為 .(請直接填結論)
(2)保證點A始終在直線MN上,正方形ABCD繞點A旋轉![]() (0<
(0<![]() <90°),過點B作BF⊥MN于點F.
<90°),過點B作BF⊥MN于點F.
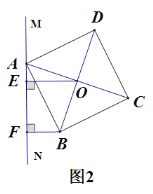
① 如圖2,當點O、B兩點均在直線MN右側時,試猜想線段AF、BF與OE之間存在怎樣的數量關系?請說明理由.
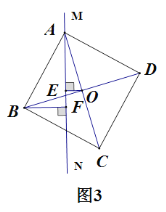
② 如圖3,當點O、B兩點分別在直線MN兩側時,此時①中結論是否依然成立呢?若成立,請直接寫出結論;若不成立,請寫出變化后的結論并證明.
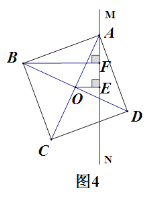
③ 當正方形ABCD繞點A旋轉到如圖4的位置時,線段AF、BF與OE之間的數量關系為 .(請直接填結論)
【答案】(1)AB=2OE;(2)①AF+BF=2OE, ②AF-BF=2OE, ③BF-AF=2OE,詳見解析.
【解析】
(1)過點B作BG⊥OE于G,可得四邊形BGEF是矩形,根據矩形的對邊相等可得EF=BG,BF=GE,根據正方形的對角線相等且互相垂直平分可得OA=OB,∠AOB=90°,再根據同角的余角相等求出∠AOE=∠OBG,然后利用“角角邊”證明△AOE和△OBG全等,根據全等三角形對應邊相等可得OG=AE,OE=BG,再根據AF-EF=AE,整理即可得證;
(2)圖2,過點B作BG⊥OE交OE的延長線于G,可得四邊形BGEF是矩形,根據矩形的對邊相等可得EF=BG,BF=GE,根據正方形的對角線相等且互相垂直平分可得OA=OB,∠AOB=90°,再根據同角的余角相等求出∠AOE=∠OBG,然后利用“角角邊”證明△AOE和△OBG全等,根據全等三角形對應邊相等可得OG=AE,OE=BG,再根據AF-EF=AE,整理即可得證;
(3)圖3,作OG⊥BF于G,可得四邊形EFGO是矩形,根據矩形的對邊相等可得EF=GO,GF=EO,根據正方形的對角線相等且互相垂直平分可得OA=OB,∠AOB=90°,再根據同角的余角相等求出∠AOE=∠BOG,然后利用“角角邊”證明△AOE和△BOG全等,根據全等三角形對應邊相等可得OG=OE,AE=BG,再根據BF-BG=GF,整理即可得證.
(1)AB=2OE
(2)①AF+BF=2OE,
證明:過點B作BH⊥OE于點H∴∠BHE=∠BHO=90°∵OE⊥MN,BF⊥MN
∴∠BFE=∠OEF=90°∴四邊形EFBH為矩形∴BF=EH,EF=BH
∵四邊形ABCD為正方形∴OA=OB,∠AOB=90°∴∠AOE+∠HOB=∠OBH+∠HOB=90°
∴∠AOE=∠OBH∴△AEO≌△OHB(AAS)∴AE=OH,OE=BH
∴AF+BF=AE+EF+BF=OH+BH+EH=OE+OE=2OE.
②AF-BF=2OE,
證明:延長OE,過點B作BH⊥OE于點H
∴∠EHB=90°
∵OE⊥MN,BF⊥MN
∴∠AEO=∠HEF=∠BFE=90°
∴四邊形HBFE為矩形∴BF=HE,EF=BH
∵四邊形ABCD是正方形
∴OA=OB,∠AOB=90°∴∠AOE+∠BOH=∠OBH+∠BOH
∴∠AOE=∠OBH∴△AOE≌△OBH(AAS)
∴AE=OH,OE=BH∴AF-BF
=AE+EF-HE=OH-HE+OE=OE+OE=2OE
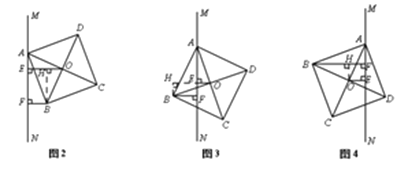
③BF-AF=2OE


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案科目:初中數學 來源: 題型:
【題目】如圖1,已知拋物線y=ax2+bx(a≠0)經過A(6,0)、B(8,8)兩點.
(1)求拋物線的解析式;
(2)將直線OB向下平移m個單位長度后,得到的直線與拋物線只有一個公共點D,求m的值及點D的坐標;
(3)如圖2,若點N在拋物線上,且∠NBO=∠ABO,則在(2)的條件下,在坐標平面內有點P,求出所有滿足△POD∽△NOB的點P坐標(點P、O、D分別與點N、O、B對應).


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨機抽取某市一年(以365天計)中的30天的日平均氣溫狀況統計如下:溫度(![]() )
)
溫度( | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
天數 | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
請根據上述數據回答下列問題:
(1)估計該城市年平均氣溫大約是多少?
(2)上表中的溫度數據的中位數是_______眾數是_________;
(3)計算該城市一年中約有幾天的日平均氣溫為![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在平面直角坐標系中,已知![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() ,
,![]() ,
,![]() .
.

(1)將![]() 向上平移
向上平移![]() 個單位長度,再向左平移
個單位長度,再向左平移![]() 個單位長度,得到
個單位長度,得到![]() ,請畫出
,請畫出![]() (點
(點![]() ,
,![]() ,
,![]() 的對應點分別為
的對應點分別為![]() ,
,![]() ,
,![]() )
)
(2)請畫出與![]() 關于
關于![]() 軸對稱的
軸對稱的![]() (點
(點![]() ,
,![]() ,
,![]() 的對應點分別為
的對應點分別為![]() ,
,![]() ,
,![]() )
)
(3)請寫出![]() ,
,![]() 的坐標
的坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.

(1)判斷∠D是否是直角,并說明理由.
(2)求四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知正比例函數![]() 與一次函數
與一次函數![]() 的圖像交于點A.
的圖像交于點A.
(1)求點A的坐標;
(2)設x軸上一點P(a,b),過點P作x軸的垂線(垂線位于點A的右側),分別交![]() 和
和![]() 的圖像于點B、C,連接OC,若BC=
的圖像于點B、C,連接OC,若BC=![]() OA,求△OBC的面積.
OA,求△OBC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,連結AE、BF.

求證:(1)AE=BF;(2)AE⊥BF.
查看答案和解析>>
科目:初中數學 來源: 題型:
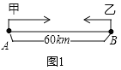
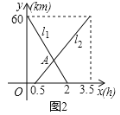
【題目】A、B兩地相距60km,甲從A地去B地,乙從B地去A地,圖中l1、l2分別表示甲、乙兩人離B地的距離y(km)與甲出發時間x(h)的函數關系圖象.
(1)根據圖象,直接寫出乙的行駛速度;
(2)解釋交點A的實際意義;
(3)甲出發多少時間,兩人之間的距離恰好相距5km;
(4)若用y3(km)表示甲乙兩人之間的距離,請在坐標系中畫出y3(km)關于時間x(h)的函數關系圖象,注明關鍵點的數據.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com