
【題目】如圖,在平面直角坐標系中,點A,B的坐標分別為A(0,α),B(b,α),且α、b滿足(a﹣2)2+|b﹣4|=0,現同時將點A,B分別向下平移2個單位,再向左平移1個單位,分別得到點A,B的對應點C,D,連接AC,BD,AB.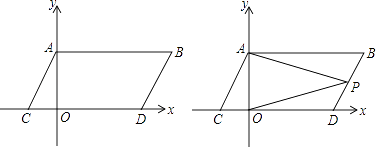
(1)求點C,D的坐標及四邊形ABDC的面積S四邊形ABCD
(2)在y軸上是否存在一點M,連接MC,MD,使S△MCD=S四邊形ABDC?若存在這樣一點,求出點M的坐標,若不存在,試說明理由.
(3)點P是線段BD上的一個動點,連接PA,PO,當點P在BD上移動時(不與B,D重合) ![]() 的值是否發生變化,并說明理由.
的值是否發生變化,并說明理由.
【答案】
(1)
解:∵(a﹣2)2+|b﹣4|=0,
∴a=2,b=4,
∴A(0,2),B(4,2).
∵將點A,B分別向下平移2個單位,再向左平移1個單位,分別得到點A,B的對應點C,D,
∴C(﹣1,0),D(3,0).
∴S四邊形ABDC=AB×OA=4×2=8
(2)
解:在y軸上存在一點M,使S△MCD=S四邊形ABCD.設M坐標為(0,m).
∵S△MCD=S四邊形ABDC,
∴ ![]() ×4|m|=8,
×4|m|=8,
∴2|m|=8,
解得m=±4.
∴M(0,4)或(0,﹣4)
(3)
解:當點P在BD上移動時, ![]() =1不變,理由如下:
=1不變,理由如下:
過點P作PE∥AB交OA于E.
∵CD由AB平移得到,則CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
∴ ![]() =1.
=1.

【解析】(1)先由非負數性質求出a=2,b=4,再根據平移規律,得出點C,D的坐標,然后根據四邊形ABDC的面積=AB×OA即可求解;(2)存在.設M坐標為(0,m),根據S△PAB=S四邊形ABDC , 列出方程求出m的值,即可確定M點坐標;(3)過P點作PE∥AB交OC與E點,根據平行線的性質得∠BAP+∠DOP=∠APE+∠OPE=∠APO,故比值為1.
【考點精析】本題主要考查了平行線的性質的相關知識點,需要掌握兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,四邊形OABC是邊長為4的正方形,點P從點O沿邊OA向點A運動,每秒運動1個單位.連結CP,過點P作PE⊥CP交AB于點D,且PE=PC,過點E作EF∥OA,交OB于點F,連結FD、BE,設點P運動的時間為![]()
![]() .
.
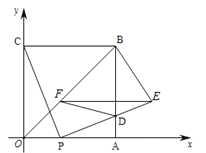
(1)點E的坐標為 (用含![]() 的代數式表示);
的代數式表示);
(2)試判斷線段EF的長度是否隨點P的運動變化而改變?并說明理由;
(3)當![]() 為何值時,四邊形BEDF的面積為
為何值時,四邊形BEDF的面積為![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
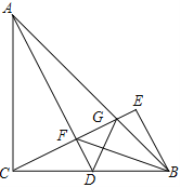
【題目】如圖,△ABC中,AC=BC,∠ACB=90°,點D為BC的中點,點E與點C關于直線AD對稱,CE與AD、AB分別交于點F、G,連接BE、BF、GD
求證:(1) △BEF為等腰直角三角形 ;(2) ∠ADC=∠BDG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大眾創業,萬眾創新,據不完全統計,2015年畢業的大學生中創業人數已經達到7490000人,將7490000這個數據用科學記數法表示為( )
A.7.49×107
B.7.49×106
C.74.9×106
D.0.749×107
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com