
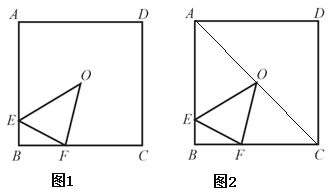
【題目】如圖1,點O為正方形ABCD 的中心,E為AB 邊上一點,F為BC邊上一點,△EBF的周長等于 BC 的長.
(1)求∠EOF 的度數.
(2)連接 OA、OC(如圖2).求證:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
【答案】(1)45°;(2)證明見解析;(3)![]()
【解析】分析:(1)、在BC上取一點G,使得CG=BE,連接OB、OC、OG,然后證明△OBE和△OCG全等,從而得出∠BOE=∠COG,∠BEO=∠CGO,OE=OG,根據三角形的周長得出EF=GF,從而得出△FOE和△GOF全等,得出∠EOF的度數;(2)、連接OA,根據點O為正方形ABCD的中心得出∠OAE=∠FCO=45°,結合∠BOE=∠COG得出∠AEO=∠COF,從而得出三角形相似;(3)、根據相似得出線段比,根據相似比求出AE和CO的關系,CF和AO的關系,從而得出答案.
詳解:解:(1)、如圖,在BC上取一點G,使得CG=BE,連接OB、OC、OG.
∵點O為正方形ABCD的中心, ∴ OB=OC,∠BOC=90°,∠OBE=∠OCG=45°.
∴△OBE≌△OCG(SAS). ∴∠BOE=∠COG,∠BEO=∠CGO,OE=OG.
∴∠EOG=90°,∵△BEF的周長等于BC的長,
∴ EF=GF. ∴△EOF≌△GOF(SSS).∴∠EOF=∠GOF=45°.
(2)、連接OA.∵ 點O為正方形ABCD的中心, ∴∠OAE=∠FCO=45°.
∵∠BOE=∠COG, ∠AEO=∠BOE+∠OBE=∠BOE+45°,
∠COF=∠COG+∠GOF=∠COG+45°. ∴ ∠AEO=∠COF,且∠OAE=∠FCO.
∴ △AOE∽△CFO.
(3)、∵△AOE∽△CFO,∴![]() =
=![]() =
=![]() .即AE=
.即AE= ![]() ×CO,CF=AO÷
×CO,CF=AO÷![]() .
.
∵OE=![]() OF,∴
OF,∴![]() =
=![]() .∴AE=
.∴AE=![]() CO,CF=
CO,CF=![]() AO. ∴
AO. ∴![]() =
=![]() .
.



科目:初中數學 來源: 題型:
【題目】某商店銷售10臺A型和20臺B型電腦的利潤為4000元,銷售20臺A型和10臺B型電腦的利潤為3500元.
(1)求每臺A型電腦和B型電腦的銷售利潤;
(2)該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的2倍,設購進A型電腦x臺,這100臺電腦的銷售總利潤為y元.
①求y關于x的函數關系式;
②該商店購進A型、B型電腦各多少臺,才能使銷售總利潤最大?
(3)實際進貨時,廠家對A型電腦出廠價下調m(0<m<100)元,且限定商店最多購進A型電腦70臺.若商店保持兩種電腦的售價不變,請你根據以上信息及(2)中條件,設計出使這100臺電腦銷售總利潤最大的進貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寒假即將到來,外出旅游的人數逐漸增多,對旅行包的需求也將增多,某店準備到生產廠家購買旅行包,該廠有甲、乙兩種新型旅行包.若購進10個甲種旅行包和20個乙種旅行包共需5600元,若購進20個甲種旅行包和10個乙種旅行包共需5200元.
(1)甲、乙兩種旅行包的進價分別是多少元?
(2)若該店恰好用了7000元購買旅行包;
①設該店購買了m個甲種旅行包,求該店購買乙種旅行包的個數;
②若該店將甲種旅行包的售價定為298元,乙種旅行包的售價定為325元,則當該店怎么樣進貨,才能獲得最大利潤,并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
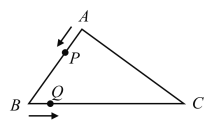
【題目】如圖,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 從點
從點![]() 出發以2個單位長度/秒的速度沿
出發以2個單位長度/秒的速度沿![]() 的方向運動,點
的方向運動,點![]() 從點
從點![]() 沿
沿![]() 的方向與點
的方向與點![]() 同時出發;當點
同時出發;當點![]() 第一次回到
第一次回到![]() 點時,點
點時,點![]() ,
,![]() 同時停止運動;用
同時停止運動;用![]() (秒)表示運動時間.
(秒)表示運動時間.
(1)當![]() 為多少時,
為多少時,![]() 是
是![]() 的中點;
的中點;
(2)若點![]() 的運動速度是
的運動速度是![]() 個單位長度/秒,是否存在
個單位長度/秒,是否存在![]() 的值,使得
的值,使得![]() ;
;
(3)若點![]() 的運動速度是
的運動速度是![]() 個單位長度/秒,當點
個單位長度/秒,當點![]() ,
,![]() 是
是![]() 邊上的三等分點時,求
邊上的三等分點時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
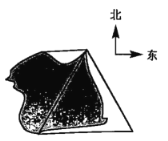
【題目】(題文)停車難已成為合肥城市病之一,主要表現在居住停車位不足,停車資源結構性失衡,中心城區供需差距大等等.如圖是張老師的車與墻平行停放的平面示意圖,汽車靠墻一側OB與墻MN平行且距離為0.8米,已知小汽車車門寬AO為 1.2 米,當車門打開角度∠AOB為40°時,車門是否會碰到墻?請說明理由.(參考數據:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某湖上風景區有兩個觀望點A,C和兩個度假村B、D;度假村D在C正西方向,度假村B在C的南偏東![]() 方向,度假村B到兩個觀望點的距離都等于2km.
方向,度假村B到兩個觀望點的距離都等于2km.
(1)在圖中標出A、B、C、D的位置,并寫出道路CD與CB的夾角.
(2)如果度假村D到C是直公路,長為1km,D到A是環湖路,度假村B到兩個觀望點的總路程等于度假村D到兩個觀望點的總路程.求出環湖路的長.
(3)根據題目中的條件,能夠判定![]() 嗎?若能,請寫出判斷過程;若不能,請你添加一個條件,判定
嗎?若能,請寫出判斷過程;若不能,請你添加一個條件,判定![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
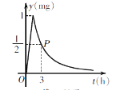
【題目】為了預防流感,某學校在休息日用藥熏消毒法對教室進行消毒. 已知藥物釋放過程中,室內每立方米空氣中的含藥量y(mg)與時間t(h)成正比;藥物釋放完畢后,y與t之間的函數解析式為y=![]() (a為常數),如圖所示. 根據圖中提供的信息,解答下列問題:
(a為常數),如圖所示. 根據圖中提供的信息,解答下列問題:
(1)寫出從釋放藥物開始,y與t之間的兩個函數解析式及相應的自變量取值范圍;
(2)據測定,當空氣中每立方米的含藥量降低到0.25mg以下時,學生方可進入教室,那么藥物釋放開始,至少需要經過多少小時,學生才能進入教室?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市移動通訊公司開設了兩種通訊業務,A類是固定用戶:先繳50元月租費,然后每通話1分鐘再付話費0.4元;B類是“神州行”用戶:使用者不繳月租費,每通話1分鐘付話費0.6元(這里均指市內通話)。如果一個月內通話時間為x分鐘,分別設A類和B類兩種通訊方式的費用為y![]() 元和y
元和y![]() 元,
元,
(1)寫出y![]() 、y
、y![]() 與x之間的函數關系式。
與x之間的函數關系式。
(2)一個月內通話多少分鐘,用戶選擇A類合算?B類呢?
(3)若某人預計使用話費150元,他應選擇哪種方式合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com