
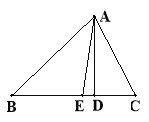
【題目】如圖,在△ABC中,AE是∠BAC的角平分線,AD是BC邊上的高,且∠B = 40, ∠C = 60,求∠CAD、∠EAD的度數。(6分)
 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為13cm,弦AB∥CD,AB=24cm,CD=10cm,則AB,CD之間的距離為( )
A.17cm
B.7cm
C.12cm
D.17cm或7cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程組和不等式解應用題:
為了響應某市的“四個一”工程,培養學生的愛國主義情懷,某校學生和帶隊老師在5月下旬某天集體乘車去參觀抗日戰爭紀念館.已知學生的數量是帶隊老師的12倍多20人,學生和老師的總人數共540人.
(1)請求出去參觀抗日戰爭紀念館學生和老師各多少人?
(2)如果學校準備租賃![]() 型大巴車和
型大巴車和![]() 型大巴車共14輛,(其中
型大巴車共14輛,(其中![]() 型大巴車最多有7輛)已知
型大巴車最多有7輛)已知![]() 型大巴車每車最多可以載35人,日租金為2000元,其中
型大巴車每車最多可以載35人,日租金為2000元,其中![]() 型大巴車每車最多可以載45人,日租金為3000元請求出最經濟的租賃車輛方案.
型大巴車每車最多可以載45人,日租金為3000元請求出最經濟的租賃車輛方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某城市為鼓勵居民節約用水,采用分段計費的方法按月計算每戶家庭的水費,月用水量不超過20m3時,按2元/m3計費;月用水量超過20m3時,超過部分按2.6元/m3計費.設每戶家庭的月用水量為xm3時,應交水費y元.
(1)試求出0≤x≤20和x>20時,y與x之間的函數關系;
(2)小明家第二季度用水量的情況如下:
月份 | 四月 | 五月 | 六月 |
用水量(m3) | 15 | 17 | 21 |
小明家這個季度共繳納水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在10×10的正方形網格中,每個小正方形的邊長為1個單位長度.△ABC的頂點都在正方形網格的格點上,且通過兩次平移(沿網格線方向作上下或左右平移)后得到△![]() ,點C的對應點是直線上的格點
,點C的對應點是直線上的格點![]() .
.
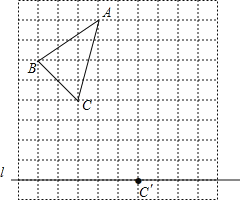
(1)畫出△![]() .
.
(2)若連接![]() 、
、![]() ,則這兩條線段之間的關系是 .
,則這兩條線段之間的關系是 .
(3)試在直線![]() 上畫出所有符合題意的格點P,使得由點
上畫出所有符合題意的格點P,使得由點![]() 、
、![]() 、
、![]() 、P四點圍成的四邊形的面積為9.
、P四點圍成的四邊形的面積為9.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,∠ABC=90°,D為AC中點,點P是線段AD上的一點,點P與點A,點D不重合),連接BP.將△ABP繞點P按順時針方向旋轉α角(0°<α<180°),得到△A1B1P,連接A1B1、BB1
(1)如圖①,當0°<α<90°,在α角變化過程中,請證明∠PAA1=∠PBB2 . 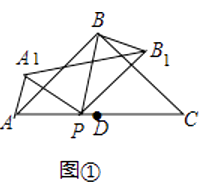
(2)如圖②,直線AA1與直線PB、直線BB1分別交于點E,F.設∠ABP=β,當90°<α<180°時,在α角變化過程中,是否存在△BEF與△AEP全等?若存在,求出α與β之間的數量關系;若不存在,請說明理由;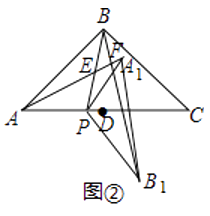
(3)如圖③,當α=90°時,點E、F與點B重合.直線A1B與直線PB相交于點M,直線BB′與AC相交于點Q.若AB= ![]() ,設AP=x,求y關于x的函數關系式.
,設AP=x,求y關于x的函數關系式.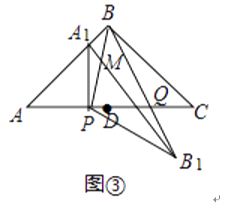
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】線段AB兩端點坐標分別為A(![]() ),B(
),B(![]() ),現將它向右平移4個單位長度,向下平移2個單位長度,得到線段A1B1,則A1、B1的坐標分別為( )
),現將它向右平移4個單位長度,向下平移2個單位長度,得到線段A1B1,則A1、B1的坐標分別為( )
A.A1(1,8),B1(-2,5)B.A1(3,2),B1(0,-1)
C.A1(-3,8),B1(-6,5)D.A1(-5,2),B1(-8,-1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com