
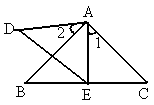
(2007·海南)如下圖,已知∠1=∠2,那么添加下列一個條件后,仍無法判定△ABC∽△ADE的是
[ ]
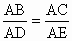
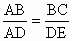
|
解析: ∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠BAC=∠DAE.∴當滿足條件A、C、D時,都能判定△ABC∽△ADE.而 ∠BAC與∠DAE不是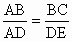 所涉及的四條邊的夾角,所以無法判定△ABC∽△ADE,故選B. 所涉及的四條邊的夾角,所以無法判定△ABC∽△ADE,故選B. |
|
題目考查的是相似三角形的判定方法. 本題從反面入手命題,找無法判定 △ABC∽△ADE的條件,實際上同時是在確定能判定△ABC∽△ADE的條件,結合相似三角形的判定方法逐一考察即可.∠BAE是兩個三角形的對應角∠BAC與∠DAE的公共部分,在∠1=∠2的基礎上能推出∠BAC=∠DAE.得出這組對應角相等后,當夾這組對應角的兩組對應邊成比例,或者還有另一組對應角相等時,就能證明這兩個三角形相似. |


科目:初中數學 來源:2007年全國中考數學試題匯編《二次函數》(08)(解析版) 題型:解答題
 x+4與x軸交于點A,與y軸交于點C,已知二次函數的圖象經過點A、C和點B(-1,0).
x+4與x軸交于點A,與y軸交于點C,已知二次函數的圖象經過點A、C和點B(-1,0). 個單位長度的速度沿折線OAC按O?A?C的路線運動,點E以每秒4個單位長度的速度沿折線OCA按O?C?A的路線運動,當D、E兩點相遇時,它們都停止運動.設D、E同時從點O出發t秒時,△ODE的面積為S.
個單位長度的速度沿折線OAC按O?A?C的路線運動,點E以每秒4個單位長度的速度沿折線OCA按O?C?A的路線運動,當D、E兩點相遇時,它們都停止運動.設D、E同時從點O出發t秒時,△ODE的面積為S.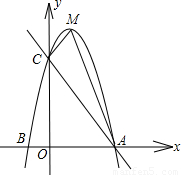
查看答案和解析>>
科目:初中數學 來源:2007年海南省中考數學試卷(解析版) 題型:解答題
 x+4與x軸交于點A,與y軸交于點C,已知二次函數的圖象經過點A、C和點B(-1,0).
x+4與x軸交于點A,與y軸交于點C,已知二次函數的圖象經過點A、C和點B(-1,0). 個單位長度的速度沿折線OAC按O?A?C的路線運動,點E以每秒4個單位長度的速度沿折線OCA按O?C?A的路線運動,當D、E兩點相遇時,它們都停止運動.設D、E同時從點O出發t秒時,△ODE的面積為S.
個單位長度的速度沿折線OAC按O?A?C的路線運動,點E以每秒4個單位長度的速度沿折線OCA按O?C?A的路線運動,當D、E兩點相遇時,它們都停止運動.設D、E同時從點O出發t秒時,△ODE的面積為S.
查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《三角形》(13)(解析版) 題型:解答題
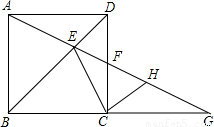
查看答案和解析>>
科目:初中數學 來源:2007年海南省中考數學試卷(解析版) 題型:填空題
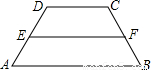
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com