如圖，在平面直角坐標系中，直線AB與y軸、x軸分別交于點A、點B，與雙曲線
交于點C（1，6）、D（3，n）兩點，
軸于點E，
軸于點F.
（1）填空：
，
；
（2）求直線AB的解析式；
（3）求證：
.
（1）
，
；（2）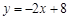
；（3）先求得直線AB與坐標軸的交點坐標，由
可得，再結合
，
即可證得
，從而可以證得結論.
解析試題分析：（1）先把（1，6）代入即可求得m的值，即可求得n的值；
（2）設直線AB的解析式為
，由圖象過點（1，6）、D（3，2）即可根據待定系數法求解；
（3）先求得直線AB與坐標軸的交點坐標，由可得，再結合，即可證得，從而可以證得結論.
解：（1），；
（2）設直線AB的解析式為：（
）
∵直線AB過點（1，6）、D（3，2）兩點
∴
，解得
∴直線AB的解析式為；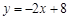
（3）在直線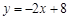中，令
，則
，令
，則
∴A（0，8），B（4，0）
∵，
∴
∵，
∴
∴.
考點：一次函數與反比例函數的交點問題
點評：一次函數與反比例函數的交點問題是初中數學的重點，是中考中比較常見的知識點，一般難度不大，需熟練掌握.
科目：初中數學 來源： 題型：解答題
定義：如圖，若雙曲線
與它的其中一條對稱軸
相交于兩點A，B，則線段AB的長稱為雙曲線的對徑．
（1）求雙曲線
的對徑;
（2）若某雙曲線對徑是
.求k的值;
（3）仿照上述定義,請你定義雙曲線
的對徑.
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
已知：如圖，在平面直角坐標系xOy中，直線AB與x軸交于點A（﹣2，0），與反比例函數在第一象限內的圖象的交于點B（2，n），連接BO，若S△AOB=4．
（1）求該反比例函數的解析式和直線AB的解析式；
（2）若直線AB與y軸的交點為C，求△OCB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
（2013年四川瀘州8分）如圖，已知函數
與反比例函數
（x＞0）的圖象交于點A．將的圖象向下平移6個單位后與雙曲線交于點B，與x軸交于點C．
（1）求點C的坐標；
（2）若
，求反比例函數的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，直線y=k1x+b（k1≠0）與雙曲線
（k2≠0）相交于A（1，m）、B（﹣2，﹣1）兩點．
（1）求直線和雙曲線的解析式．
（2）若A1（x1，y1），A2（x2，y2），A3（x3，y3）為雙曲線上的三點，且x1＜x2＜0＜x3，請直接寫出y1，y2，y3的大小關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，反比例函數
的圖象與一次函數y=mx+b的圖象交于A（1，3），B（n，﹣1）兩點．
（1）求反比例函數與一次函數的解析式；
（2）根據圖象回答：當x取何值時，反比例函數的值大于一次函數的值．
（3）求△AOB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：計算題
下圖是交警在某個路口統計的某時段來往車輛的車速情況．（單位：千米/時）
（1）車速的眾數是多少？
（2）計算這些車輛的平均數度；
（3）車速的中位數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：填空題
要把一個正方體分割成8個小正方體，至少需要切3刀，因為這8個小正方體都只有三個面現成的，其它三個面必須用刀切3次才能切出來，那么，要把一個正方體分割成27個小正方體，至少需要要刀切 次，分割成64個小正方體，至少需要用刀切 次。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
