Question

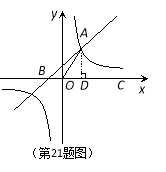
【題目】如圖，在平面直角坐標系中，一次函數的圖象與反比例函數在第一象限內的圖象交于點A，與x軸交于點B，線段OA＝5，C為x軸正半軸上一點，且∠AOC＝．

（1）求一次函數和反比例函數的解析式；

（2）求△AOB的面積．

Answer 1

【答案】（1），（2）6

【解析】

試題分析：（1）過A點作AD⊥x軸于點D，根據已知的∠AOC的正弦值以及OA的長，利用三角形函數的定義求出AD的長，再利用勾股定理求出OD的長，即可得到點A的坐標，把點A的坐標分別代入到反比例函數和一次函數的解析式中即可確定出兩函數的解析式；

（2）根據x軸上點的特征，令一次函數的y=0，求出x的值，確定出點B的坐標，得到線段OB的長，利用三角形的面積公式即可求出三角形AOB的面積．

試題解析：(1)過A點作AD⊥x軸于點D，

∵sin∠AOC＝

∴AD＝4.

由勾股定理得：DO=3，

∵點A在第一象限

∴點A的坐標為(3，4)

將A的坐標為(3，4)代入y＝，得，∴m＝12

∴該反比例函數的解析式為

將A的坐標為(3，4)代入得：

∴一次函數的解析式是

(2)在中，令y＝0，即x＋2=0，∴x=

∴點B的坐標是 ∴OB＝3，又DA=4

∴所以△AOB的面積為OB×AD=×3×4=6．