【題目】如圖所示，在某海域，一般指揮船在C處收到漁船在B處發出的求救信號，經確定，遇險拋錨的漁船所在的B處位于C處的南偏西45°方向上，且BC=60海里；指揮船搜索發現，在C處的南偏西60°方向上有一艘海監船A，恰好位于B處的正西方向.于是命令海監船A前往搜救，已知海監船A的航行速度為30海里/小時，問漁船在B處需要等待多長時間才能得到海監船A的救援？（參考數據：
，
，
結果精確到0.1小時）
【答案】1.0小時.
【解析】延長AB交南北軸于點D，則AB⊥CD于點D，通過解直角三角形BDC和ADC，求出BD、CD和AD的長，繼而求出AB的長，從而可以解決問題.
如圖，因為A在B的正西方，延長AB交南北軸于點D，則AB⊥CD于點D．
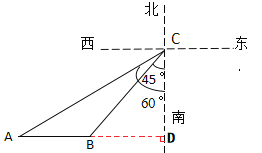
∵∠BCD=45°，BD⊥CD，
∴BD=CD．
在Rt△BDC中，∵cos∠BCD=
，BC=60海里，
即cos45°=
，解得CD=
海里，
∴BD=CD=海里．
在Rt△ADC中，∵tan∠ACD=
即 tan60°=
=
，解得AD=
海里，
∵AB=AD－BD，
∴AB=－=30（
）海里．
∵海監船A的航行速度為30海里/小時，
則漁船在B處需要等待的時間為 
=
=≈2.45－1.41=1.04≈1.0小時，
∴漁船在B處需要等待約1.0小時．
名校課堂系列答案科目：初中數學 來源： 題型：
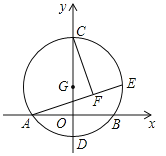
【題目】如圖，以
為圓心，半徑為
的圓與
軸交于
、
兩點，與
軸交于
、
兩點，點
為⊙
上一動點，
于
，則弦
的長度為__________，當點在⊙上運動的過程中，線段
的長度的最小值為__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，點D在CE上，AF⊥CB，垂足為F.
(1)若AC＝10，求四邊形ABCD的面積；
(2)求證：CE＝2AF.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AE是中線，AD是角平分線，AF是高，填空：
（1）BE＝ ＝
（2）∠BAD＝
（3）∠AFB＝ ＝90°
（4）S△ABC＝ S△ABE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點A、D、C、F在同一條直線上，AD=CF，AB=DE，BC=EF.
(1)求證：ΔABC≌△DEF；
(2)若∠A=55°，∠B=88°，求∠F的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料并完成任務：
點
在數軸上分別表示有理數
；兩點之間的距離表示為
．
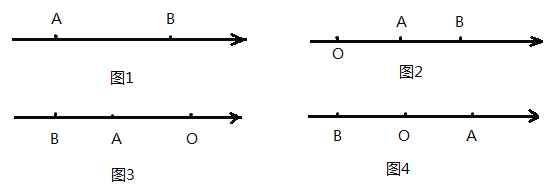
當兩點中有一點在原點時，不妨設點
在原點，如圖1所示， 
；
當兩點都不在原點時，分三種情況，
情況一：如圖2所示，點都在原點的右側，
；
情況二：如圖3所示，點都在原點左側，
；
情況三：如圖4所示，點在原點的兩邊，
；
綜上所述，若點在數軸上分別表示有理數，則數軸上兩點之間的距離為
．
任務一：數軸上表示2和5的兩點之間的距離是________，數軸上表示-2和-5的兩點之間的距離是________，數軸上表示3和-1的兩點之間的距離是________．
任務二：點
在數軸上分別表示有理數
，那么到
的距離與到
的距離之和可表示為_________(用含絕對值的式子表示)．如果
，那么
為________．
任務三：當
取最小值時， =________， 
=________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把矩形紙片ABCD沿對角線折疊，設重疊部分為△EBD，那么下列說法錯誤的是（ ）
A. △EBD是等腰三角形，EB=ED B. 折疊后∠ABE和∠C′BD一定相等
C. 折疊后得到的圖形是軸對稱圖形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，O為坐標原點，點A（8,0）動點P從A出發以每秒2個單位長度的速度沿線段AO向終點O運動，同時動點Q從O出發以相同速度沿y軸正半軸運動，點P到達點O，兩點同時停止運動.
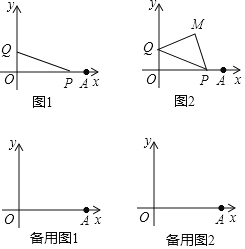
（1）當t= 時，∠OPQ=45°；
（2）如圖2，以PQ為斜邊在第一象限作等腰Rt△PQM，求M點坐標；
（3）在（2）的條件下，點R位x軸負半軸上一點，且
,點M關于PQ的對稱點為N，求t為何值時，△ONR為等腰直角三角形；
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
