


 AP,以及,∠APD=60°,可以證明∠PCA=90°,在直角△ACD中根據勾股定理即可求得直徑AD的長,從而求得半徑的長.
AP,以及,∠APD=60°,可以證明∠PCA=90°,在直角△ACD中根據勾股定理即可求得直徑AD的長,從而求得半徑的長. 解:由切割線定理得PB•PA=PC•PD,
解:由切割線定理得PB•PA=PC•PD, =4
=4
 AD=2
AD=2 .
.

 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
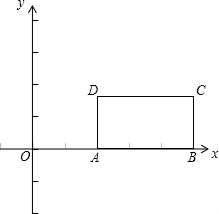 已知:矩形ABCD(字母順序如圖)的邊長AB=3,AD=2,將此矩形放在平面直角坐標系xOy中,使AB在x軸正半軸上,而矩形的其它兩個頂點在第一象限,且直線y=
已知:矩形ABCD(字母順序如圖)的邊長AB=3,AD=2,將此矩形放在平面直角坐標系xOy中,使AB在x軸正半軸上,而矩形的其它兩個頂點在第一象限,且直線y=| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
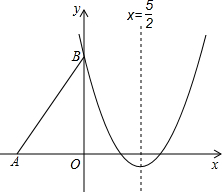 (2012•蘭州)如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y=
(2012•蘭州)如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:2013年貴州省貴陽市開陽縣中考數學模擬試卷(解析版) 題型:解答題
 x2+bx+c經過點B,且頂點在直線x=
x2+bx+c經過點B,且頂點在直線x= 上.
上.
查看答案和解析>>
科目:初中數學 來源:2013年4月中考數學模擬試卷(61)(解析版) 題型:解答題
 x2+bx+c經過點B,且頂點在直線x=
x2+bx+c經過點B,且頂點在直線x= 上.
上.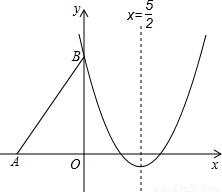
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com