(2003•紹興)已知二次函數的圖象的頂點坐標為(-2,-3),且圖象過點(-3,-2).
(1)求此二次函數的解析式;
(2)設此二次函數的圖象與x軸交于A,B兩點,O為坐標原點,求線段OA,OB的長度之和.
【答案】分析:(1)頂點坐標為(-2,-3),且圖象過點(-3,-2).可用頂點式待定系數法求此二次函數的解析式;(2)求線段OA,OB的長度之和,因為二次函數的圖象與x軸交于A、B兩點,A、B兩點的縱坐標為0,則有點A、B的橫坐標是方程x2+4x+1=0的兩根,根據一元二次方程根與系數的關系即可求出.
解答:解:
(1)∵函數圖象的頂點坐標為(-2,-3),
∴設此二次函數的解析式為y=a(x+2)2-3(2分)
又∵圖象過點(-3,-2),
∴-2=a(-3+2)2-3,
∴a=1(2分)
∴此二次函數的解析式是y=(x+2)2-3(1分)
(2)設點A,B的橫坐標分別為x1,x2,
則x1,x2是方程x2+4x+1=0的兩根,
∴x1+x2=-4,x1•x2=1,(2分)
∴x1<0,x2<0
∴OA+OB=|x1|+|x2|=-x1-x2=-(x1+x2)=4.(3分)
點評:本題考查了頂點式待定系數法求出二次函數解析式,及一元二次方程根與系數的關系.



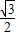 PD,求△POD與△PDG的面積之比;
PD,求△POD與△PDG的面積之比;