
【題目】如圖,△ABC中,∠ACB=90°,AC<BC,將△ABC沿EF折疊,使點A落在直角邊BC上的D點處,設EF與AB、AC邊分別交于點E、F,如果折疊后△CDF與△BDE均為等腰三角形,那么∠B=_____.

【答案】30°
【解析】
先確定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因為不確定△BDE是以那兩條邊為腰的等腰三角形,故需討論,①DE=DB,②BD=BE,③DE=BE,然后分別利用角的關系得出答案即可.
解:∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
設∠DAE=x°,由對稱性可知,AF=FD,AE=DE,
∴∠FDA=![]() ∠CFD=22.5°,∠DEB=2x°,
∠CFD=22.5°,∠DEB=2x°,
分類如下:
①當DE=DB時,如圖1所示:
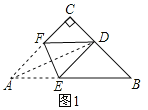
∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.
此時∠B=2x=45°,
∵AC<BC,
∴∠B=45°不成立;
②當BD=BE時,如圖2所示:
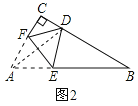
則∠B=(180°﹣4x)°,∠CAD=22.5°.
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,
此時∠B=(180﹣4x)°=30°.
③DE=BE時,則∠B=![]() (180﹣2x)°,
(180﹣2x)°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+![]() (180﹣2x)°,
(180﹣2x)°,
此方程無解.
∴DE=BE不成立.
綜上所述,∠B=30°.
故答案為:30°.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,![]() ,連結AC,過點C作直線l∥AB,點P是直線l上的一個動點,直線PA與⊙O交于另一點D,連結CD,設直線PB與直線AC交于點E.
,連結AC,過點C作直線l∥AB,點P是直線l上的一個動點,直線PA與⊙O交于另一點D,連結CD,設直線PB與直線AC交于點E.
(1)求∠BAC的度數;
(2)當點D在AB上方,且CD⊥BP時,求證:PC=AC;
(3)在點P的運動過程中
①當點A在線段PB的中垂線上或點B在線段PA的中垂線上時,求出所有滿足條件的∠ACD的度數;
②設⊙O的半徑為6,點E到直線l的距離為3,連結BD,DE,直接寫出△BDE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的角平分線,DF⊥AB,垂足為F,DE=DG,△ADG和△AED的面積分別為50和38,則△EDF的面積為( )

A. 6B. 12C. 4D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是過A的一條直線, 且B、C在AE的異側, BD⊥AE于D, CE⊥AE于E.

(1)求證: BD=DE+CE.
(2)若直線AE繞A點旋轉到圖②位置時(BD<CE), 其余條件不變, 問BD與DE、CE的數量關系如何? 請給予證明;
(3)若直線AE繞A點旋轉到圖③位置時(BD>CE), 其余條件不變, 問BD與DE、CE的數量關系如何? 請直接寫出結果, 不需證明.
(4)根據以上的討論,請用簡潔的語言表達BD與DE,CE的數量關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸,y軸分別交于B,C兩點,拋物線
與x軸,y軸分別交于B,C兩點,拋物線![]() 過點B,C.
過點B,C.
(1)求b、c的值;
(2)若點D是拋物線在x軸下方圖象上的動點,過點D作x軸的垂線,與直線BC相交于點E.當線段DE的長度最大時,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的菱形ABCD中,∠A=60°,M是邊AD的中點,N是AB上一動點(不與A、B重合),將△AMN沿MN所在直線翻折得到△A1MN,連接A1C,畫出點N從A到B的過程中A1的運動軌跡,A1C的最小值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃一次性購買排球和籃球,每個籃球的價格比排球貴30元;購買2個排球和3個籃球共需340元.
(1)求每個排球和籃球的價格:
(2)若該校一次性購買排球和籃球共60個,總費用不超過3800元,且購買排球的個數少于39個.設排球的個數為m,總費用為y元.
①求y關于m的函數關系式,并求m可取的所有值;
②在學校按怎樣的方案購買時,費用最低?最低費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
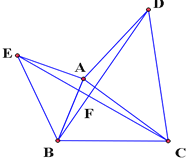
【題目】如圖,已知△ABC,分別以AB,AC為直角邊,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,連結BD,CE交于點F,設AB=m,BC=n.
(1)求證:∠BDA=∠ECA.
(2)若m=![]() ,n=3,∠ABC=75°,求BD的長.
,n=3,∠ABC=75°,求BD的長.
(3)當∠ABC=____時,BD最大,最大值為____(用含m,n的代數式表示)
(4)試探究線段BF,AE,EF三者之間的數量關系。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com