
【題目】甲、乙兩個批發店銷售同一種蘋果,甲批發店的價格為每千克6元.在乙批發店,一次購買數量不超過![]() 時,價格為每千克7元;一次購買數量超過
時,價格為每千克7元;一次購買數量超過![]() 時,其中有
時,其中有![]() 的價格為每千克7元,超過
的價格為每千克7元,超過![]() 部分的價格為每千克5元,設小王在同個批發店一次購買蘋果的數量為
部分的價格為每千克5元,設小王在同個批發店一次購買蘋果的數量為![]()
![]() .
.
(1)填表:
一次購買蘋果的數量(單位: | 20 | 50 | 100 | … |
甲批發店花費(單位:元) | 300 | … | ||
乙批發店花費(單位:元) | 350 | … |
(2)分別用含![]() 的代數式表示甲、乙批發店所花費的錢數.
的代數式表示甲、乙批發店所花費的錢數.
(3)如果小王在同一個批發店一次購買蘋果的數量為![]() ,通過計算說明他在甲、乙兩個批批發店所花費的錢數少?
,通過計算說明他在甲、乙兩個批批發店所花費的錢數少?
【答案】(1)120 ,600,140,600;(2)y1=6x(x>0); y2=7x(0<x≤50)y2=5x+100(x>50);(3)乙批發店花費少.
【解析】
(1)根據題意,甲批發店花費 y1(元)=6×購買數量x(千克);6×20=120,6×100=600;而乙批發店花費 y2(元),當一次購買數量不超過50kg時,y2=7××20=140元;一次購買數量超過50kg時,y2=7×50+5(100-50)=600元.
(2)根據題意,甲批發店花費 y1(元)=6×購買數量x(千克);而乙批發店花費 y2(元)在一次購買數量不超過50kg時,y2(元)=7×購買數量x(千克);一次購買數量超過50kg時,y2(元)=7×50+5(x-50);即:花費 y2(元)是購買數量x(千克)的分段函數.
(3)求出當x=120時,兩店所對應的y的值,比較得出結論.實際是已知函數值求相應的自變量的值.
(1)甲批發店:6×20=120,6×100=600;乙批發店:7××20=140元,7×50+5(100-50)=600元.
故依次填寫:120 ,600,140,600;
(2)y1=6x(x>0)
當0<x≤50時,y2=7x(0<x≤50)
當x>50時,y2=7×50+5(x-50)=5x+100(x>50)
因此y1,y2與x的函數解析式為:y1=6x(x>0);![]()
(3)當![]() 時,
時,![]() 元,
元,
![]() 元.
元.
∵![]() ,
,
∴乙批發店花費少.
答:乙批發店花費少.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】某中學數學活動小組為了調查居民的用水情況,從某社區的![]() 戶家庭中隨機抽取了
戶家庭中隨機抽取了![]() 戶家庭的月用水量,結果如下表所示:
戶家庭的月用水量,結果如下表所示:
月用水量(噸) |
|
|
|
|
|
|
|
戶數 |
|
|
|
|
|
|
|
![]() 求這
求這![]() 戶家庭月用水量的平均數、眾數和中位數;
戶家庭月用水量的平均數、眾數和中位數;
![]() 根據上述數據,試估計該社區的月用水量;
根據上述數據,試估計該社區的月用水量;
![]() 由于我國水資源缺乏,許多城市常利用分段計費的方法引導人們節約用水,即規定每個家庭的月基本用水量為
由于我國水資源缺乏,許多城市常利用分段計費的方法引導人們節約用水,即規定每個家庭的月基本用水量為![]() (噸),家庭月用水量不超過
(噸),家庭月用水量不超過![]() (噸)的部分按原價收費,超過
(噸)的部分按原價收費,超過![]() (噸)的部分加倍收費.你認為上述問題中的平均數、眾數和中位數中哪一個量作為月基本用水量比較合適?簡述理由.
(噸)的部分加倍收費.你認為上述問題中的平均數、眾數和中位數中哪一個量作為月基本用水量比較合適?簡述理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實踐與探索
(1)填空: ![]() =______;
=______; ![]() =______;
=______; ![]() =______;
=______; ![]() ______;
______;
(2)觀察第(1)題的計算結果回答: ![]() 一定等于
一定等于![]() 嗎?你發現其中的規律了嗎?請把你觀察到的規律歸納出來 。
嗎?你發現其中的規律了嗎?請把你觀察到的規律歸納出來 。
(3)利用你總結的規律計算: ![]() .(2<x<3)
.(2<x<3)
查看答案和解析>>
科目:初中數學 來源: 題型:
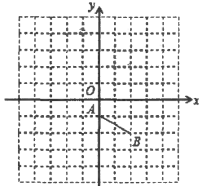
【題目】如圖,在正方形網格中,每個小正方形的邊長為1個單位長度.平面直角坐標系![]() 的原點
的原點![]() 在格點上,
在格點上,![]() 軸、
軸、![]() 軸都在格線上.線段
軸都在格線上.線段![]() 的兩個端點也在格點上.
的兩個端點也在格點上.
(1)若將線段![]() 繞點
繞點![]() 逆時針旋轉90°得到線段
逆時針旋轉90°得到線段![]() ,試在圖中畫出線段
,試在圖中畫出線段![]() .
.
(2)若線段![]() 與線段
與線段![]() 關于
關于![]() 軸對稱,請畫出線段
軸對稱,請畫出線段![]() .
.
(3)若點![]() 是此平面直角坐標系內的一點,當點
是此平面直角坐標系內的一點,當點![]() 四邊圍成的四邊形為平行四邊形 時,請你直接寫出點
四邊圍成的四邊形為平行四邊形 時,請你直接寫出點![]() 的坐標(寫出一個即可).
的坐標(寫出一個即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形ABCD與CEFG,如圖放置,點B,C,E共線,點C,D,G共線,連接AF,取AF的中點H,連接GH.若BC=EF=2,CD=CE=1,則GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
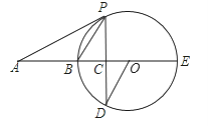
【題目】如圖,BE是圓O的直徑,A在EB的延長線上,AP為圓O的切線,P為切點,弦PD垂直于BE于點C.
(1)求證:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圓O的半徑及tan∠APB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是甲、乙兩車在某時段速度隨時間變化的圖象,下列結論錯誤的是( )
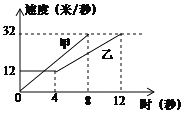
A. 乙前4秒行駛的路程為48米 B. 兩車到第3秒時行駛的路程相等
C. 在0到8秒內甲的速度每秒增加4米/秒 D. 在4至8秒內甲的速度都大于乙的速度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,AB=8cm,BC=10cm,點P從點A開始沿AB邊向點B以1cm/s的速度移動,點Q從點B開始沿BC邊向點C以2cm/s的速度移動.如果P、Q分別從A、B同時出發,當一個點到達終點時,另一個點隨之停止.設運動時間為x秒,△PBQ的面積為ycm2.
(1)求y與x的函數關系式,寫出x的取值范圍;
(2)求運動多少秒時,△PBQ的面積為12cm2;
(3)求運動多少秒時,△PBQ的面有最大值.最大值是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解學生的安全意識情況,在全校范圍內隨機抽取部分學生進行問卷調查,根據調查結果,把學生的安全意識分成“淡薄”、“一般”、“較強”、“很強”四個層次,并繪制成如下兩幅尚不完整的統計圖.

根據以上信息,解答下列問題:
(1)這次調查一共抽取了 名學生,其中安全意識為“很強”的學生占被調查學生總數的百分比是 ;
(2)請將條形統計圖補充完整;
(3)該校有1800名學生,現要對安全意識為“淡薄”、“一般”的學生強化安全教育,根據調查結果,估計全校需要強化安全教育的學生約有 名.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com