【答案】
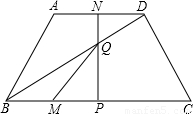
分析:(1)分別過點A,D作BC邊上的高,交BC邊于E,F,由于四邊形ABCD是等腰梯形,可得出BE=CF=(BC-AD)÷2=1,又由AB=DC=2,根據勾股定理可得點D到BC的距離DF=
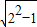
=
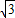
(2)根據(1)得出的DF的值,可求出BD的長為2
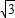
,那么三角形BDC是個直角三角形,且∠C=60°,∠DBC=30°,如果QM∥AB,可得出∠PMQ度數也是60°,可先表示出MP的長,然后根據∠PQM的度數表示出PQ,然后根據QP∥DF,得出關于QP,DF,BP,BF的比例關系式,DF的值是定值,可表示出BP,BF,這樣就可求出t的值.
(3)要分兩種情況進行討論
①當N在AD上時,關鍵是求出PQ,可在直角三角形BPQ中,先表示出BP,然后根據∠QBP的度數即可求出PQ的長,然后根據三角形的面積公式即可得出S,t的函數關系式.
②N在AB上時,還是要先求出PQ的值,可先表示出BN,然后在直角三角形BNP中,表示出BP,進而在直角三角形BPQ中,用BP表示出PQ,即可根據三角形的面積公式得出S,t的函數關系式.
(4)也要分兩種情況進行討論.
第一種情況,當N在AD上時,①當∠BMQ=90°時,那么M,P重合,于是就有BM+ND+FC=BC,即2t+1=4,即可得出t的值.
②當∠BQM=90°時,可先在直角三角形NDQ中,用ND的長,表示出NQ,然后根據求出的D到BC的距離,即可表示出PQ,這時PQ的第一種表示方法.第二種表示方法是,在直角三角形BMQ中,用BM表示出QM,然后在直角三角形QPM中,表示出PQ,然后可讓這兩個表示PQ的式子相等,即可得出此時的t的值.
第二種情況,當N在AB上時,此時只有∠BQM=90°,方法同②,也是通過不同的表示PQ的方法來得出t的值,方法同(3)②.
解答:解:(1)
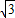
(2)過A作AE⊥BC于E,過D作DF⊥BC于F,則四邊形AEFD是矩形.
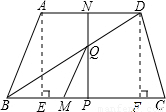
BE=CF=
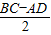
=1.
直角三角形CFD中,CF=1,CD=2,cos∠C=

∴∠C=60°,DF=
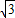
.
∴∠ABE=∠C=60°
∵QM∥AB
∴∠QMP=60°
∵BM=t,PF=ND=t,FC=1,BC=4
∴PM=3-2t,BP=3-t.
直角三角形QPM中,∠QMP=60°,PM=3-2t,QP=
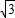
(3-2t).
∵QP⊥BC,DF⊥BC
∴QP∥DF,
∴△BQP∽△BDF,
∴
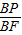
=
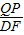
,即
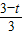
=
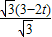
∴5t=6,即t=1.2(s)
當t=1.2s時,QM∥AB
(3)當0<t≤2時,三角形BDF中,BF=3,DF=
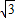
,
∴BD=2
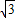
三角形BCD中,CD=2,BD=2
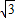
,BC=4,
因此BD
2+CD
2=BC
2,
即三角形BDC是直角三角形,且∠BDC=90°,∠DBC=30°.
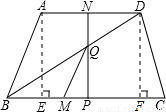
直角三角形BQP中,BP=3-t,∠DBC=30°,
∴PQ=
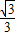
(3-t)
因此:S=

×t×
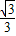
(3-t)=-
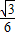
t
2+
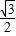
t
當2<t<4時,直角三角形NBP中,∠ABC=60°,BN=4-t,
∴BP=
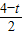
.
在直角三角形BPQ中,∠DBC=30°,BP=
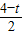
,
∴QP=
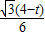
因此:S=

×t×

=-
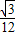
t
2+
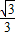
t
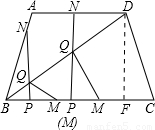
(4)當0<t≤2時,即N在AD上時,分兩種情況進行討論:
①當∠BMQ=90°,即M與P點重合,那么BM+PF+CF=BM+ND+CF=2t+1=4
解得:t=1.5s.
②當∠BQM=90°,在直角三角形NQD中,ND=t,∠ADB=∠DBC=30°,
∴NQ=
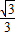
t.
∵NP=
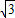
∴QP=
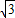
-
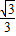
t
在直角三角形BQM中,∠DBC=30°,BM=t
∴QM=

t
在直角三角形QPM中,∠QMP=60°,QM=

t
∴QP=
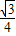
t
∴
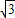
-
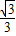
t=
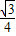
t.
解得t=
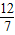
s.
當2<t<4時,∠BQM=90°
直角三角形BNP中,BN=4-t,∠ABC=60°,
∴BP=
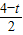
,
∴PM=BM-BP=t-
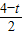
=
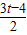
在直角三角形BPQ中,∠DBC=30°,BP=
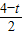
∴PQ=
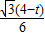
直角三角形QPM中,∠QMP=60°,PM=
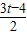
∴PQ=
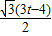
因此
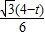
=
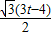
,
解得t=1.6s,與此時t的取值范圍不符,
因此這種情況不成立.
綜上所述,當t=1.5s或
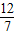
s,△BMQ是直角三角形.
點評:本題主要考查了等腰梯形的性質,相似三角形的性質等知識點,要注意的是(3)(4)都要分情況討論,不要漏解.

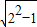 =
=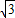
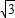 ,那么三角形BDC是個直角三角形,且∠C=60°,∠DBC=30°,如果QM∥AB,可得出∠PMQ度數也是60°,可先表示出MP的長,然后根據∠PQM的度數表示出PQ,然后根據QP∥DF,得出關于QP,DF,BP,BF的比例關系式,DF的值是定值,可表示出BP,BF,這樣就可求出t的值.
,那么三角形BDC是個直角三角形,且∠C=60°,∠DBC=30°,如果QM∥AB,可得出∠PMQ度數也是60°,可先表示出MP的長,然后根據∠PQM的度數表示出PQ,然后根據QP∥DF,得出關于QP,DF,BP,BF的比例關系式,DF的值是定值,可表示出BP,BF,這樣就可求出t的值.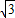

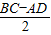 =1.
=1.
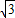 .
.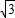 (3-2t).
(3-2t).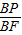 =
=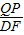 ,即
,即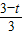 =
=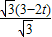
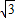 ,
,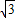
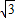 ,BC=4,
,BC=4,
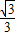 (3-t)
(3-t) ×t×
×t×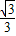 (3-t)=-
(3-t)=-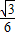 t2+
t2+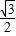 t
t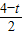 .
.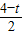 ,
,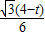
 ×t×
×t× =-
=-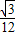 t2+
t2+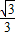 t
t
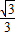 t.
t.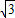
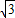 -
-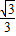 t
t t
t t
t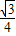 t
t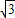 -
-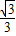 t=
t=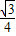 t.
t.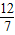 s.
s.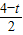 ,
,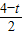 =
=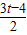
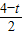
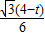
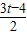
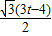
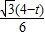 =
=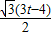 ,
,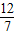 s,△BMQ是直角三角形.
s,△BMQ是直角三角形.

 已知:如圖,四邊形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四邊形ABCD繞直線AB旋轉一周,則所得幾何體的表面積是多少?
已知:如圖,四邊形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四邊形ABCD繞直線AB旋轉一周,則所得幾何體的表面積是多少?