
【題目】已知關于![]() 的一元二次方程x2-4x+k+1=0
的一元二次方程x2-4x+k+1=0
(1)若![]() =-1是方程的一個根,求k值和方程的另一根;
=-1是方程的一個根,求k值和方程的另一根;
(2)設x1,x2是關于x的方程x2-4x+k+1=0的兩個實數根,是否存在實數k,使得x1x2>x1+x2成立?請說明理由.
【答案】(1)k= -6 ,方程的另一根是5.
(2)不存在.理由見解析.
【解析】
試題分析:(1)把![]() =-1代入方程即可求出k的值,利用根與系數的關系可求出方程的另一根;(2)利用根與系數的關系可得x1+x2=4,x1x2=k+1,代入x1x2>x1+x2求出k的取值范圍,然后利用Δ≥0,求出k的取值范圍,比較即可.
=-1代入方程即可求出k的值,利用根與系數的關系可求出方程的另一根;(2)利用根與系數的關系可得x1+x2=4,x1x2=k+1,代入x1x2>x1+x2求出k的取值范圍,然后利用Δ≥0,求出k的取值范圍,比較即可.
試題解析:(1)把![]() =-1代入方程x2-4x+k+1=0 ,得1+4+k+1=0 ,解得k= -6 ,設另一個根為x,則x+(-1)=4,所以x=5,即方程的另一根是5.(4分)
=-1代入方程x2-4x+k+1=0 ,得1+4+k+1=0 ,解得k= -6 ,設另一個根為x,則x+(-1)=4,所以x=5,即方程的另一根是5.(4分)
( 2 )不存在.理由:由題意得Δ=16-4(k+1)≥0,解得k≤3.∵x1,x2是一元二次方程的兩個實數根,∴x1+x2=4,x1x2=k+1,由x1x2>x1+x2得k+1>4,∴k>3,∴不存在實數k使得x1x2>x1+x2成立.(4分)


科目:初中數學 來源: 題型:
【題目】一家商店進行門店升級需要裝修,裝修期間暫停營業,若請甲乙兩個裝修組同時施工,8天可以完成,需付費用共3520元;若先請甲組單獨做6天,再請乙組單獨做12天可以完成,需付費用3480元,問:
![]() 甲、乙兩組工作一天,商店各應付多少錢?
甲、乙兩組工作一天,商店各應付多少錢?
![]() 已知甲組單獨完成需12天,乙組單獨完成需24天,單獨請哪個組,商店所需費用最少?
已知甲組單獨完成需12天,乙組單獨完成需24天,單獨請哪個組,商店所需費用最少?
![]() 裝修完畢第二天即可正常營業,且每天仍可盈利200元
裝修完畢第二天即可正常營業,且每天仍可盈利200元![]() 即裝修前后每天盈利不變
即裝修前后每天盈利不變![]() ,你認為商店應如何安排施工更有利?說說你的理由
,你認為商店應如何安排施工更有利?說說你的理由![]() 可用
可用![]() 問的條件及結論
問的條件及結論![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,點
,點![]() 分別是
分別是![]() 軸,
軸,![]() 軸上兩個動點,直角邊
軸上兩個動點,直角邊![]() 交
交![]() 軸于點
軸于點![]() ,斜邊
,斜邊![]() 交
交![]() 軸于點
軸于點![]() .
.
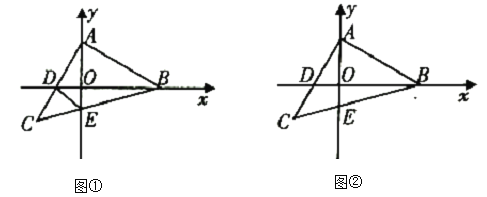
(1)如圖①,當等腰![]() 運動到使點
運動到使點![]() 恰為
恰為![]() 中點時,連接
中點時,連接![]() ,求證:
,求證:![]() ;
;
(2)如圖②,當等腰![]() 運動到使
運動到使![]() 時,
時,![]() 點的橫坐標為
點的橫坐標為![]() ,
,![]() .在
.在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 為等腰三角形?若存在,請直接寫出點
為等腰三角形?若存在,請直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理是數學史上非常重要的一個定理.早在![]() 多年以前,人們就開始對它進行研究,至今已有幾百種證明方法.在歐幾里得編的《原本》中證明勾股定理的方法如下,請同學們仔細閱讀并解答相關問題:如圖,分別以
多年以前,人們就開始對它進行研究,至今已有幾百種證明方法.在歐幾里得編的《原本》中證明勾股定理的方法如下,請同學們仔細閱讀并解答相關問題:如圖,分別以![]() 的三邊為邊長,向外作正方形
的三邊為邊長,向外作正方形![]() 、
、![]() 、
、![]() .
.
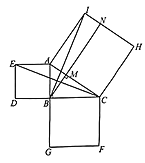
(1)連接![]() 、
、![]() ,求證:
,求證:![]()
(2)過點![]() 作
作![]() 的垂線,交
的垂線,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
①試說明四邊形![]() 與正方形
與正方形![]() 的面積相等;
的面積相等;
②請直接寫出圖中與正方形![]() 的面積相等的四邊形.
的面積相等的四邊形.
(3)由第(2)題可得:正方形![]() 的面積
的面積![]() 正方形
正方形![]() 的面積
的面積![]() _______________的面積,即在
_______________的面積,即在![]() 中,
中,![]() __________________.
__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩個箱子,其中甲箱內有![]() 顆球,分別標記號碼
顆球,分別標記號碼![]() ,且號碼為不重復的整數,乙箱內沒有球.已知小育從甲箱內拿出
,且號碼為不重復的整數,乙箱內沒有球.已知小育從甲箱內拿出![]() 顆球放入乙箱后,乙箱內球的號碼的中位數為
顆球放入乙箱后,乙箱內球的號碼的中位數為![]() .若此時甲箱內有
.若此時甲箱內有![]() 顆球的號碼小于
顆球的號碼小于![]() ,有
,有![]() 顆球的號碼大于
顆球的號碼大于![]() ,若他們的中位數都為
,若他們的中位數都為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】要建一個如圖所示的面積為300![]() 的長方形圍欄,圍欄總長50m,一邊靠墻(墻長25m),
的長方形圍欄,圍欄總長50m,一邊靠墻(墻長25m),

(1)求圍欄的長和寬;
(2)能否圍成面積為400 ![]() 的長方形圍欄?如果能,求出該長方形的長和寬,如果不能請說明理由。
的長方形圍欄?如果能,求出該長方形的長和寬,如果不能請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛慢車和一輛快車沿相同的路線從A地到B地,所行駛的路程與時間的函數圖形如圖所示,下列說法正確的有( )
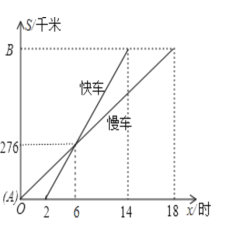
①快車追上慢車需6小時;②慢車比快車早出發2小時;③快車速度為46km/h;④慢車速度為46km/h; ⑤A、B兩地相距828km;⑥快車從A地出發到B地用了14小時
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用一根長度為![]() 的細繩圍成一個等腰三角形.
的細繩圍成一個等腰三角形.
(1)如果所圍等腰三角形的腰長是底邊長的2倍,則此時的底邊長度是多少?
(2)所圍成的等腰三角形的腰長不可能等于![]() ,請簡單說明原因.
,請簡單說明原因.
(3)若所圍成的等腰三角形的腰長為![]() ,請求出
,請求出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司購買了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的單價比
型芯片的單價比![]() 型芯片的單價少9元,已知該公司用3120元購買
型芯片的單價少9元,已知該公司用3120元購買![]() 型芯片的條數與用4200元購買
型芯片的條數與用4200元購買![]() 型芯片的條數相等.
型芯片的條數相等.
(1)求該公司購買的![]() 、
、![]() 型芯片的單價各是多少元?
型芯片的單價各是多少元?
(2)若兩種芯片共購買了200條,且購買的總費用為6280元,求購買了多少條![]() 型芯片?
型芯片?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com