
【題目】如圖,△ABC面積為1,第一次操作:分別延長AB,BC,CA至點A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,順次連接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分別延長A1B1 , B1C1 , C1A1至點A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 順次連接A2 , B2 , C2 , 得到△A2B2C2 , …按此規律,要使得到的三角形的面積超過2010,最少經過( )次操作.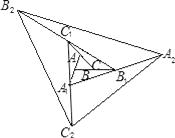
A.6
B.5
C.4
D.3
【答案】C
【解析】解:△ABC與△A1BB1底相等(AB=A1B),高為1:2(BB1=2BC),故面積比為1:2,
∵△ABC面積為1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可證S△A2B2C2=7S△A1B1C1=49,
第三次操作后的面積為7×49=343,
第四次操作后的面積為7×343=2401.
故按此規律,要使得到的三角形的面積超過2010,最少經過4次操作.
故選C.
【考點精析】通過靈活運用數與式的規律,掌握先從圖形上尋找規律,然后驗證規律,應用規律,即數形結合尋找規律即可以解答此題.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數學 來源: 題型:
【題目】下列各組線段長度成比例的是( )
A.1㎝,2㎝,3㎝,4㎝
B.1㎝,3㎝,4.5㎝,6.5㎝
C.1.1㎝,2.2㎝,3.3㎝,4.4㎝
D.1㎝,2㎝,2㎝,4㎝
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個多邊形紙片按圖示的剪法剪去一個內角后,得到一個內角和為2340°的新多邊形,則原多邊形的對角線條數為( ) 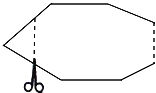
A.77
B.90
C.65
D.104
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設A(﹣2,y1),B(1,y2),C(2,y3)是拋物線y=3(x+1)2+4m(m為常數)上的三點,則y1,y2,y3的大小關系為( )
A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y3<y2<y1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別交線段BC,AC于點D,E,過點D作DF⊥AC,垂足為F,線段FD,AB的延長線相交于點G.
(1)求證:DF是⊙O的切線;
(2)若CF=1,DF=![]() ,求圖中陰影部分的面積.
,求圖中陰影部分的面積.
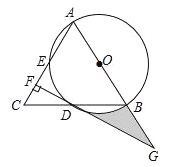
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在大樓AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小紅在斜坡下的點C處測得樓頂B的仰角為60°,在斜坡上的點D處測得樓頂B的仰角為45°,其中點A、C、E在同一直線上.
(1)求斜坡CD的高度DE;
(2)求大樓AB的高度(結果保留根號)
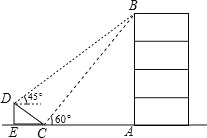
查看答案和解析>>
科目:初中數學 來源: 題型:
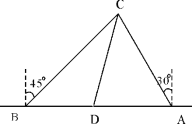
【題目】(本題滿分9分)為了維護海洋權益,新組建的國家海洋局加大了在南海的巡邏力度。一天,我兩艘海監船剛好在我某島東西海岸線上的A、B兩處巡邏,同時發現一艘不明國籍的船只停在C處海域。如圖所示,AB=60![]() 海里,在B處測得C在北偏東45的方向上,A處測得C在北偏西30的方向上,在海岸線AB上有一燈塔D,測得AD=120
海里,在B處測得C在北偏東45的方向上,A處測得C在北偏西30的方向上,在海岸線AB上有一燈塔D,測得AD=120![]() 海里。
海里。
(1)(4分)分別求出A與C及B與C的距離AC,BC(結果保留根號)
(2)(5分)已知在燈塔D周圍100海里范圍內有暗礁群,我在A處海監船沿AC前往C處盤查,途中有無觸礁的危險?(參考數據:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“愛我永州”中學生演講比賽中,五位評委分別給甲、乙兩位選手的評分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
則下列說法中錯誤的是( )
A.甲、乙得分的平均數都是8
B.甲得分的眾數是8,乙得分的眾數是9
C.甲得分的中位數是9,乙得分的中位數是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中數學 來源: 題型:
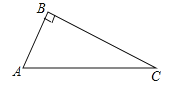
【題目】如圖,已知△ABC中,∠ABC=90°.
(1)尺規作圖:按下列要求完成作圖(保留作圖痕跡,請標明字母)
①作線段AC的垂直平分線l,交AC于點O;
②連接BO并延長,在BO的延長線上截取OD,使得OD=OB;
③連接DA、DC.
(2)判斷四邊形ABCD的形狀,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com