【題目】計算：
（1）9﹣（﹣5）﹣（+2）+（﹣4）﹣5
（2）﹣|﹣7
|+（+3
）﹣5
（3）
﹣|﹣1|﹣（+2
）﹣（﹣2.75）
（4）﹣9÷3+（﹣
）×12+（﹣3）2
（5）﹣5×（﹣3
）+（﹣9）×（3）+17×（﹣3）
（6）（
）÷（﹣
）
【答案】（1）3；（2）﹣9
；（3）﹣
；（4）8；（5）﹣75；（6）﹣31．
【解析】
（1）利用減法法則變形，計算即可求出值；
（2）先計算絕對值，再利用加減法法則計算即可求出值；
（3）先計算絕對值，再利用加減法法則計算即可求出值；
（4）先計算乘方運算，再計算乘法運算，最后算加減運算即可求出值．
（5）逆用乘法分配律即可求出值．
（6）先把除法化成乘法，再根據乘法分配律即可求出值．
（1）9﹣（﹣5）﹣（+2）+（﹣4）﹣5
＝9+5+（﹣2）+（﹣4）+（﹣5）
＝3；
（2）﹣|﹣7
|+（+3
）﹣5
＝﹣7+3+（﹣5）
＝﹣7
+3
+（﹣5）
＝﹣9；
（3）
﹣|﹣1|﹣（+2
）﹣（﹣2.75）
＝
+（﹣2）+2
＝﹣；
（4）﹣9÷3+（
）×12+（﹣3）2
＝﹣3+
×12+9
＝﹣3+2+9
＝8；
（5）﹣5×（﹣3
）+（﹣9）×（3）+17×（﹣3）
＝5×3﹣9×3﹣17×3
＝（5﹣9﹣17）×3
＝（﹣21）×
＝﹣75；
（6）（
）÷（﹣
）
＝（）×（﹣60）
＝（﹣40）+5+4
＝﹣31．
科目：初中數學 來源： 題型：
【題目】在一個不透明的盒子中放有四張分別寫有數字1、2、3、4的紅色卡片和三張分別寫有數字1、2、3的藍色卡片，卡片除顏色和數字外其它完全相同。
（1）從中任意抽取一張卡片，則該卡片上寫有數字1的概率是；
（2）將3張藍色卡片取出后放入另外一個不透明的盒子內，然后在兩個盒子內各任意抽取一張卡片，以紅色卡片上的數字作為十位數，藍色卡片上的數字作為個位數組成一個兩位數，求這個兩位數大于22的概率。（請利用樹狀圖或列表法說明）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分線分別交AB和AC于點D,E.
(1)求證:AE=2CE;
(2)連接CD,請判斷△BCD的形狀,并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】a，b分別是數軸上兩個不同點A，B所表示的有理數，且|a|＝5，|b|＝2，A，B兩點在數軸上的位置如圖所示：
(1)試確定數a，b；
(2)A，B兩點相距多少個單位長度？
(3)若C點在數軸上，C點到B點的距離是C點到A點距離的
，求C點表示的數；
(4)點P從A點出發，先向左移動1個單位長度，再向右移動2個單位長度，再向左移動3個單位長度，再向右移動4個單位長度，依次操作2 019次后，求P點表示的數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在Rt△ABC中，∠ACB=90°，AC=2，BC=4．點D是線段BC上的一個動點．點D與點B、C不重合，過點D作DE⊥BC交AB于點E，將△ABC沿著直線DE翻折，使點B落在直線BC上的F點．
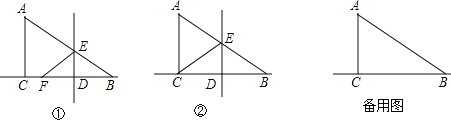
（1）設∠BAC=α（如圖①），求∠AEF的大小；（用含α的代數式表示）
（2）當點F與點C重合時（如圖②），求線段DE的長度；
（3）設BD=x，△EDF與△ABC重疊部分的面積為S，試求出S與x之間函數關系式，并寫出自變量x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數
（a＜0）圖象與x軸的交點A、B的橫坐標分別為﹣3，1，與y軸交于點C，下面四個結論：
①16a﹣4b+c＜0；②若P（﹣5，y1），Q（
，y2）是函數圖象上的兩點，則y1＞y2；③a=﹣
c；④若△ABC是等腰三角形，則b=﹣
．其中正確的有______（請將結論正確的序號全部填上）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】撫順某中學為了解八年級學生的體能狀況，從八年級學生中隨機抽取部分學生進行體能測試，測試結果分為A，B，C，D四個等級．請根據兩幅統計圖中的信息回答下列問題：
（1）本次抽樣調查共抽取了多少名學生？
（2）求測試結果為C等級的學生數，并補全條形圖；
（3）若該中學八年級共有700名學生，請你估計該中學八年級學生中體能測試結果為D等級的學生有多少名？
（4）若從體能為A等級的2名男生2名女生中隨機的抽取2名學生，做為該校培養運動員的重點對象，請用列表法或畫樹狀圖的方法求所抽取的兩人恰好都是男生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某蔬菜加工公司先后兩批次收購蒜薹(tái)共100噸．第一批蒜薹價格為4000元/噸；因蒜薹大量上市，第二批價格跌至1000元/噸．這兩批蒜薹共用去16萬元．
(1)求兩批次購進蒜薹各多少噸；
(2)公司收購后對蒜薹進行加工，分為粗加工和精加工兩種：粗加工每噸利潤400元，精加工每噸利潤1000元．要求精加工數量不多于粗加工數量的三倍．為獲得最大利潤，精加工數量應為多少噸？最大利潤是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
