
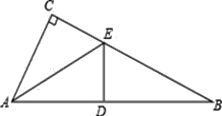
【題目】已知:如圖,在△ABC中,∠C=90°,AE是△ABC的角平分線;ED平分∠AEB,交AB于點D;∠CAE=∠B.
(1)如果AC=3cm,求AB的長度;
(2)猜想:ED與AB的位置關系,并證明你的猜想。
【答案】(1)6cm;(2)ED⊥AB.理由見解析.
【解析】試題分析:(1)先由角平分線的定義及已知條件得出∠CAE=∠EAB=∠B,再根據直角三角形兩銳角互余得出∠CAE+∠EAB+∠B=3∠B=90°,那么∠B=30°,根據30°角所對的直角邊等于斜邊的一半得出AB=2AC=6cm;
(2)先由∠EAB=∠B,根據等角對等邊得出EB=EA,又ED平分∠AEB,根據等腰三角形三線合一的性質得到ED⊥AB.
試題解析:(1)∵AE是△ABC的角平分線,
∴∠CAE=∠EAB,
∵∠CAE=∠B,
∴∠CAE=∠EAB=∠B.
∵在△ABC中,∠C=90°,
∴∠CAE+∠EAB+∠B=3∠B=90°,
∴∠B=30°;
又∵∠C=90°,AC=3cm,
∴AB=2AC=6cm .
(2)猜想:ED⊥AB.理由如下:
∵∠EAB=∠B,
∴EB=EA,
∵ED平分∠AEB,
∴ED⊥AB.
故答案為(1)6cm (2)猜想:ED⊥AB.


科目:初中數學 來源: 題型:
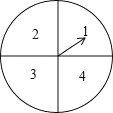
【題目】某超市計劃在“十周年”慶典當天開展購物抽獎活動,凡當天在該超市購物的顧客,均有一次抽獎的機會,抽獎規則如下:將如圖所示的圓形轉盤平均分成四個扇形,分別標上1,2,3,4四個數字,抽獎者連續轉動轉盤兩次,當每次轉盤停止后指針所指扇形內的數為每次所得的數(若指針指在分界線時重轉);當兩次所得數字之和為8時,返現金20元;當兩次所得數字之和為7時,返現金15元;當兩次所得數字之和為6時返現金10元.
(1)試用樹狀圖或列表的方法表示出一次抽獎所有可能出現的結果;
(2)某顧客參加一次抽獎,能獲得返還現金的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據國家發改委實施“階梯電價”的有關文件要求,某市結合地方實際,決定對居民生活用電實行“階梯電價”收費,具體收費標準見表:
一戶居民一個月用電量的范圍 | 電費價格(單位:元/度) |
不超過200度 | a |
超過200度的部分 | b |
已知4月份,該市居民甲用電250度,交電費130元;居民乙用電400度,交電費220元.
(1)求出表中a和b的值;
(2)實行“階梯電價”收費以后,該市一戶居民月用電多少度時,其當月的平均電價每度不超過0.56元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C,D在同一條直線上,點E,F分別在直線AD的兩側,且AE=DF,∠A=∠D,AB=DC.
(1)求證:四邊形BFCE是平行四邊形;
(2)若AD=10,DC=3,∠EBD=60°,則BE= 時,四邊形BFCE是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式: ![]() ,
, ![]() ,
, ![]() ,
,
將以上三個等式兩邊分別相加得: ![]() =1﹣
=1﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() .
.
(1)猜想并寫出: ![]() = .
= .
(2)直接寫出下列各式的計算結果:
① ![]() +…+
+…+ ![]() =;
=;
② ![]() …+
…+ ![]() =;
=;
(3)探究并計算: ![]() …+
…+ ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將二次函數y=x2的圖象向下平移2個單位,再向右平移3個單位,則平移后的二次函數的解析式為( )
A.y=x2﹣2
B.y=x2+2
C.y=(x+3)2+2
D.y=(x﹣3)2﹣2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com