
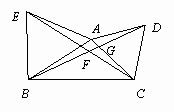
如圖,以△ABC的邊AB、AC向外作等邊△ABE和△ACD,連接BD、CE,線段CE和BD有什么數量關系?證明你的結論;能否求出∠DFC的度數?
|
因為△ ABE和△ACD是等邊三角形所以∠ DAC=∠EAB=60°,AE=AB,AD=AC所以∠ EAC=∠DAB在△ AEC和△ABD中
所以△ AEC≌△ABD所以∠ BDA=∠ACE又∠ CGF=∠DGA所以∠ DFC=∠DAC=60°. |
| 經過分析可以發現只需要證明線段BD和CE所在的△AEC和△ABD全等即可,根據等邊三角形的性質可以得到AC=AD,AE=AB,∠DAC=∠EAB=60°,進而得到∠EAC=∠BAD,根據SAS得到△AEC≌△ABD,于是結論成立;根據可以得到∠BDA=∠ACE,又∠CGF=∠DGA(對頂角),可以得到∠DFC=60°,問題解決. |


科目:初中數學 來源: 題型:
 26、如圖,以△ABC的邊AB、AC為邊的等邊三角ABD和等邊三角形ACE,四邊形ADFE是平行四邊形.
26、如圖,以△ABC的邊AB、AC為邊的等邊三角ABD和等邊三角形ACE,四邊形ADFE是平行四邊形.查看答案和解析>>
科目:初中數學 來源: 題型:
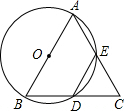 如圖,以△ABC的邊AB為直徑作⊙O,交BC于D點,交AC于E點,BD=DE
如圖,以△ABC的邊AB為直徑作⊙O,交BC于D點,交AC于E點,BD=DE | BD |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2011•峨眉山市二模)如圖,以△ABC的邊AB為直徑作⊙O,BC與⊙O交于D,D是BC的中點,過D作DE⊥AC,交AC于點E.
(2011•峨眉山市二模)如圖,以△ABC的邊AB為直徑作⊙O,BC與⊙O交于D,D是BC的中點,過D作DE⊥AC,交AC于點E.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2010•黔東南州)如圖,以△ABC的邊BC為直徑作⊙O分別交AB,AC于點F.點E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔東南州)如圖,以△ABC的邊BC為直徑作⊙O分別交AB,AC于點F.點E,AD⊥BC于D,AD交于⊙O于M,交BE于H.查看答案和解析>>
科目:初中數學 來源: 題型:
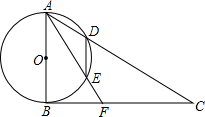 如圖,以△ABC的邊AB為直徑的⊙O交AC于點D,弦DE∥AB,∠C=∠BAF
如圖,以△ABC的邊AB為直徑的⊙O交AC于點D,弦DE∥AB,∠C=∠BAF| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com