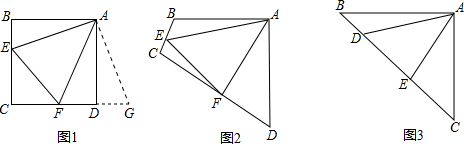
如圖1,點C、B分別為拋物線C1:y1=x2+1,拋物線C2:y2=a2x2+b2x+c2的頂點.分別過點B、C作x軸的平行線,交拋物線C1、C2于點A、D,且AB=BD.
(1)求點A的坐標:
(2)如圖2,若將拋物線C1:“y1=x2+1”改為拋物線“y1=2x2+b1x+c1”.其他條件不變,求CD的長和a2的值;
(3)如圖2,若將拋物線C1:“y1=x2+1”改為拋物線“y1=4x2+b1x+c1”,其他條件不變,求b1+b2的值______
【答案】
分析:(1)連接AC、BC,根據二次函數圖象的對稱性可得AC=BC,BC=BD,再根據已知條件AB=BD,可以證明得到△ABC是等邊三角形,所以∠ACE=30°,然后設AE=m,根據等邊三角形的性質求出CE的長,再根據拋物線C
1:y
1=x
2+1求出點C的坐標,從而表示出點A的坐標,然后把點A的坐標代入拋物線C
1的解析式,然后解關于m的一元二次方程求出m的值,代入即可得到點A的坐標;
(2)過點C作CE⊥AB于點E,設拋物線y
1=2x
2+b
1x+c
1=2(x-h
1)
2+k
1,然后表示出C的坐標,再設AE=m,根據等邊三角形的性質求出CE的長度,從而得到點A的坐標,把點A的坐標代入拋物線C
1,整理后解關于m的一元二次方程,再根據(1)的結論即可求出CD的長;根據CD的長求出CE的長度,然后表示出點B的坐標,根據點B在是拋物線C
2的頂點,從而得到拋物線C
2的頂點式解析式,然后根據點C在拋物線C
2上,把點C的坐標代入拋物線C
2的解析式,整理求解即可得到a
2的值;
(3)根據(1)(2)的結論可知,a
2=-a
1,然后利用兩拋物線的對稱軸表示出CD的長度,再根據(1)(2)的求解過程可得CD=2×
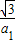
,然后代入進行計算即可得解.
解答:解:(1)如圖,連接AC、BC,設直線AB交y軸于點E,
∵AB∥x軸,CD∥x軸,C、B為拋物線C
1、C
2的頂點,
∴AC=BC,BC=BD,
∵AB=BD,
∴AC=BC=AB,
∴△ABC是等邊三角形,
∴∠ACE=30°,
設AE=m,
則CE=
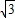
AE=
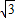
m,
∵y
1=x
2+1,
∴點C的坐標為(0,1),
∴點A的坐標為(-m,1+
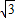
m),
∵點A在拋物線C
1上,
∴(-m)
2+1=1+
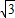
m,
整理得m
2-
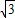
m=0,
解得m
1=
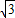
,m
2=0(舍去),
∴點A的坐標為(-
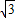
,4);
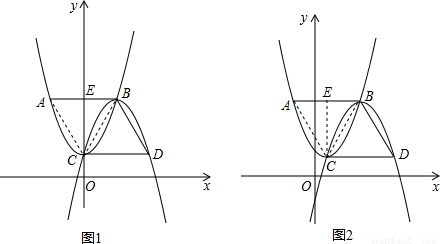
(2)如圖2,連接AC、BC,過點C作CE⊥AB于點E,
設拋物線y
1=2x
2+b
1x+c
1=2(x-h
1)
2+k
1,
∴點C的坐標為(h
1,k
1),
設AE=m,
∴CE=
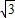
m,
∴點A的坐標為(h
1-m,k
1+
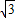
m),
∵點A在拋物線y
1=2(x-h
1)
2+k
1上,
∴2(h
1-m-h
1)
2+k
1=k
1+
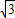
m,
整理得,2m
2=
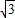
m,
解得m
1=
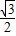
,m
2=0(舍去),
由(1)同理可得,CD=BD=BC=AB,
∵AB=2AE=
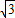
,
∴CD=
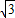
,
即CD的長為
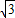
,
根據題意得,CE=
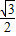
BC=
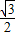
×
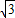
=

,
∴點B的坐標為(h
1+
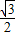
,k
1+

),
又∵點B是拋物線C
2的頂點,
∴y
2=a
2(x-h
1-
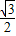
)
2+k
1+

,
∵拋物線C
2過點C(h
1,k
1),
∴a
2(h
1-h
1-
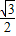
)
2+k
1+

=k
1,
整理得

a
2=-

,
解得a
2=-2,
即a
2的值為-2;
(3)根據(2)的結論,a
2=-a
1,

CD=-
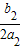
-(-
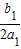
)=
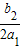
+
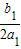
=
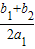
,
根據(1)(2)的求解,CD=2×
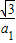
,
∴b
1+b
2=2
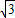
.
點評:本題是對二次函數的綜合考查,主要利用了二次函數的對稱性,等邊三角形的性質,二次函數的頂點式解析式與一般解析式之間的轉化,對同學們的能力要求較高,靈活性較強,規律總結比較重要,總體而言,本題難度較大,是道難得的好題.

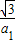 ,然后代入進行計算即可得解.
,然后代入進行計算即可得解.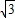 AE=
AE=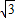 m,
m,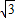 m),
m),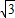 m,
m,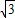 m=0,
m=0,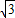 ,m2=0(舍去),
,m2=0(舍去),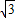 ,4);
,4);
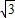 m,
m,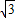 m),
m),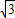 m,
m,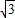 m,
m,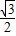 ,m2=0(舍去),
,m2=0(舍去), ,
, ,
, ,
, BC=
BC=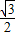 ×
×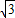 =
= ,
,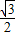 ,k1+
,k1+ ),
),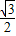 )2+k1+
)2+k1+ ,
,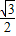 )2+k1+
)2+k1+ =k1,
=k1, a2=-
a2=- ,
, CD=-
CD=-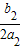 -(-
-(-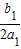 )=
)=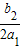 +
+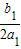 =
=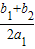 ,
,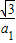 ,
,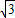 .
.

 閱讀快車系列答案
閱讀快車系列答案