
【題目】在學習解直角三角形以后,某興趣小組測量了旗桿的高度.如圖,某一時刻,旗桿AB的影子一部分落在水平地面L的影長BC為5米,落在斜坡上的部分影長CD為4米.測得斜CD的坡度i=1:![]() .太陽光線與斜坡的夾角∠ADC=80°,則旗桿AB的高度_____.(精確到0.1米)(參考數據:sin50°=0.8,tan50°=1.2,
.太陽光線與斜坡的夾角∠ADC=80°,則旗桿AB的高度_____.(精確到0.1米)(參考數據:sin50°=0.8,tan50°=1.2,![]() =1.732)
=1.732)

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
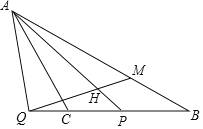
【題目】如圖,已知等腰△ABC,∠ACB=120°,P是線段CB上一動點(與點C,B不重合),連接AP,延長BC至點Q,使得∠PAC=∠QAC,過點Q作射線QH交線段AP于H,交AB于點M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示線段QC和BM之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在內角不確定的△ABC中,AB=AC,點E、F分別在AB、AC上,EF∥BC,平行移動EF,如果梯形EBCF有內切圓.
當![]() =
=![]() 時,sinB=
時,sinB=![]() ;
;
當![]() =
=![]() 時,sinB=
時,sinB=![]() (提示:
(提示:![]() =
=![]() );當
);當![]() =
=![]() 時,sinB=
時,sinB=![]() .
.
(1)請你根據以上所反映的規律,填空:當![]() =
=![]() 時,sinB的值等于______;
時,sinB的值等于______;
(2)當![]() =
=![]() 時(n是大于1的自然數),請用含n的代數式表示sinB=______,并畫出圖形、寫出已知、求證和證明過程.
時(n是大于1的自然數),請用含n的代數式表示sinB=______,并畫出圖形、寫出已知、求證和證明過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
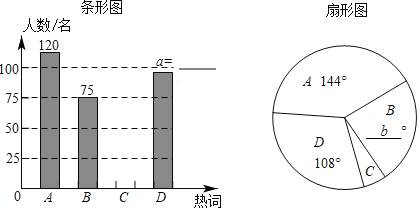
【題目】網絡時代,新興詞匯層出不窮.為了解大眾對網絡詞匯的理解,某興趣小組舉行了一個“我是路人甲”的調查活動:選取四個熱詞A:“硬核人生”,B:“好嗨哦”,C:“雙擊666”,D:“杠精時代”在街道上對流動人群進行了抽樣調查,要求被調查的每位只能勾選一個最熟悉的熱詞,根據調查結果,該小組繪制了如下的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了 名路人.
(2)補全條形統計圖;
(3)扇形圖中的b= .
查看答案和解析>>
科目:初中數學 來源: 題型:
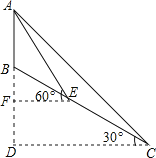
【題目】如圖,小山頂上有一信號塔AB,山坡BC的傾角為30°,現為了測量塔高AB,測量人員選擇山腳C處為一測量點,測得塔頂仰角為45°,然后順山坡向上行走100米到達E處,再測得塔頂仰角為60°,求塔高AB.(結果保留整數![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:探究函數y=x+![]() 的圖象和性質.
的圖象和性質.
小華根據學習函數的方法和經驗,進行了如下探究,下面是小華的探究過程,請補充完整:
(1)函數的自變量x的取值范圍是:____;
(2)如表是y與x的幾組對應值,請將表格補充完整:
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
(3)如圖,在平面直角坐標系中描點并畫出此函數的圖象;
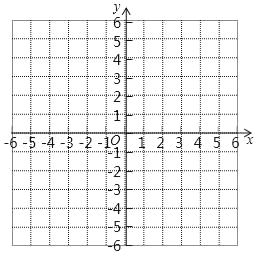
(4)進一步探究:結合函數的圖象,寫出此函數的性質(一條即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著天氣的逐漸炎熱(如圖1),遮陽傘在我們的日常生活中隨處可見如圖2所示,遮陽傘立柱OA垂直于地面,當將遮陽傘撐開至OD位置時,測得∠ODB=45°,當將遮陽傘撐開至OE位置時,測得∠OEC=30°,且此時遮陽傘邊沿上升的豎直高度BC為20cm,求若當遮陽傘撐開至OE位置時傘下陰涼面積最大,求此時傘下半徑EC的長.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC,AB=AC,BD是∠ABC的角平分線,EF是BD的中垂線,且分別交BC于點E,交AB于點F,交BD于點K,連接DE,DF.
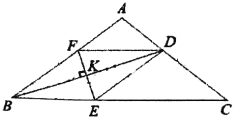
(1)證明:DE//AB;
(2)若CD=3,求四邊形BEDF的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店準備進一批季節性小家電,每個進價為40元,經市場預測,銷售定價為50元,可售出400個;定價每增加1元,銷售量將減少10個.設每個定價增加x元.
(1)寫出售出一個可獲得的利潤是多少元(用含x的代數式表示)?
(2)商店若準備獲得利潤6000元,并且使進貨量較少,則每個定價為多少元?應進貨多少個?
(3)商店若要獲得最大利潤,則每個應定價多少元?獲得的最大利潤是多少?
【答案】(1)x+10元;(2)每個定價為70元,應進貨200個.(3)每個定價為65元時得最大利潤,可獲得的最大利潤是6250元.
【解析】試題分析:(1)根據利潤=銷售價-進價列關系式,(2)總利潤=每個的利潤×銷售量,銷售量為400-10x,列方程求解,根據題意取舍,(3)利用函數的性質求最值.
試題解析:由題意得:(1)50+x-40=x+10(元),
(2)設每個定價增加x元,
列出方程為:(x+10)(400-10x)=6000,解得:x1=10,x2=20,要使進貨量較少,則每個定價為70元,應進貨200個,
(3)設每個定價增加x元,獲得利潤為y元,
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,當x=15時,y有最大值為6250,所以每個定價為65元時得最大利潤,可獲得的最大利潤是6250元.
【題型】解答題
【結束】
24
【題目】猜想與證明:
如圖1,擺放矩形紙片ABCD與矩形紙片ECGF,使B、C、G三點在一條直線上,CE在邊CD上,連接AF,若M為AF的中點,連接DM、ME,試猜想DM與ME的關系,并證明你的結論.
拓展與延伸:
(1)若將”猜想與證明“中的紙片換成正方形紙片ABCD與正方形紙片ECGF,其他條件不變,則DM和ME的關系為 .
(2)如圖2擺放正方形紙片ABCD與正方形紙片ECGF,使點F在邊CD上,點M仍為AF的中點,試證明(1)中的結論仍然成立.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com