
 的等邊三角形,其中O是坐標原點,頂點A在x軸的
的等邊三角形,其中O是坐標原點,頂點A在x軸的 正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.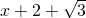 .
. EO.
EO.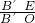 ,
, ;
; ,
, ).
). ,而我們還可以通過∠EOB′的正弦函數得出OE,EB′的比例關系,然后根據這兩個關系可得出OE,B′E的長,進而可求出OB′的長.也就得出了點B′和E點的坐標.
,而我們還可以通過∠EOB′的正弦函數得出OE,EB′的比例關系,然后根據這兩個關系可得出OE,B′E的長,進而可求出OB′的長.也就得出了點B′和E點的坐標.

科目:初中數學 來源: 題型:
| 3 |
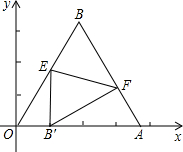 正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,△OAB是邊長為2+
如圖所示,△OAB是邊長為2+| 3 |
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江西省撫州市金溪二中九年級(上)第三次月考數學試卷 (解析版) 題型:解答題
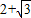 的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.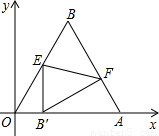
查看答案和解析>>
科目:初中數學 來源:2013年廣東省汕尾市中考數學模擬試卷(一)(解析版) 題型:解答題
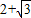 的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
查看答案和解析>>
科目:初中數學 來源:2009年廣東省潮州市潮安縣松昌實驗學校中考數學一模試卷(解析版) 題型:解答題
 的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com