
【題目】如圖,![]() 是等邊三角形,點
是等邊三角形,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,
,![]() 、
、![]() 相交于點
相交于點![]() ,連接
,連接![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,正確的結論有( )
,正確的結論有( )
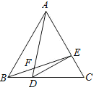
A. 4個 B. 3個 C. 2個 D. 1個
【答案】A
【解析】
本題是開放題,對結論進行一一論證,從而得到答案.
①利用△ABD≌△BCE,再用三角形的一個外角等于與它不相鄰的兩個內角和,即可證∠AFE=60°;
②從CD上截取CM=CE,連接EM,證△CEM是等邊三角形,可證明DE⊥AC;
③△BDF∽△ADB,由相似比則可得到CE2=DFDA;
④只要證明了△AFE∽△BAE,即可推斷出AFBE=AEAC.
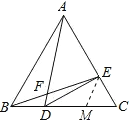
∵△ABC是等邊三角形,
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°.
∵BD=![]() BC,CE=
BC,CE=![]() AC,
AC,
∴BD=EC.
∴△ABD≌△BCE.
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°,
∴∠ABE+∠CBE=60°.
∵∠AFE是△ABF的外角,
∴∠AFE=60°.
∴①是對的;
如圖,從CD上截取CM=CE,連接EM,則△CEM是等邊三角形,
∴EM=CM=EC.
∵EC=![]() CD,
CD,
∴EM=CM=DM.
∴∠CED=90°.
∴DE⊥AC,
∴②是對的;
由前面的推斷知△BDF∽△ADB.
∴BD:AD=DF:DB.
∴BD2=DFDA.
∴CE2=DFDA.
∴③是對的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE.
∴AFBE=AEAC.
∴④是正確的.
故答案選A.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() .
.
(1)如圖1,若直線![]() 與
與![]() 相交于
相交于![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,連接
,連接![]() 并延長
并延長![]() 至
至![]() ,使得
,使得![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,證明:
,證明:![]() .
.
(2)如圖2,若直線![]() 與
與![]() 的延長線相交于
的延長線相交于![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,連接
,連接![]() 并延長
并延長![]() 至
至![]() ,使得
,使得![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于
的延長線于![]() ,探究:
,探究:![]() 、
、![]() 、
、![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
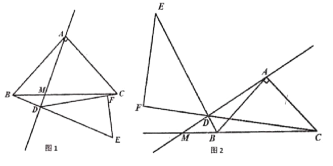
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為美化校園,計劃對面積為![]() 的區域進行綠化,安排甲、乙兩個工程隊完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化的面積的2倍,并且在獨立完成面積為
的區域進行綠化,安排甲、乙兩個工程隊完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化的面積的2倍,并且在獨立完成面積為![]() 區域的綠化時,甲隊比乙隊少用4天。
區域的綠化時,甲隊比乙隊少用4天。
(1)求甲、乙兩工程隊每天能完成綠化的面積分別是多少![]() ?
?
(2)若學校每天需付給甲隊的綠化費用為0.35萬元,乙隊為0.25萬元,要使這次的綠化總費用不超過8萬元,至少應安排甲隊工作多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),一架云梯AB斜靠在一豎直的墻上,云梯的頂端A距地面15米,梯子的長度比梯子底端B離墻的距離大5米.
(1)這個云梯的底端B離墻多遠?
(2)如圖(2),如果梯子的頂端下滑了8m(AC的長),那么梯子的底部在水平方向右滑動了多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點![]() 是線段
是線段![]() 的中點,
的中點,![]() ,
,![]() .
.
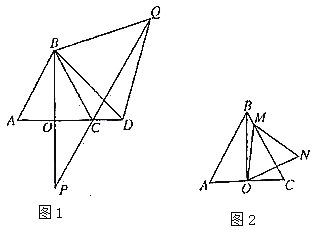
(1)如圖1,若![]() ,求證
,求證![]() 是等邊三角形;
是等邊三角形;
(2)如圖1,在(1)的條件下,若點![]() 在射線
在射線![]() 上,點
上,點![]() 在點
在點![]() 右側,且
右側,且![]() 是等邊三角形,
是等邊三角形,![]() 的延長線交直線
的延長線交直線![]() 于點
于點![]() ,求
,求![]() 的長度;
的長度;
(3)如圖2,在(1)的條件下,若點![]() 在線段
在線段![]() 上,
上,![]() 是等邊三角形,且點
是等邊三角形,且點![]() 沿著線段
沿著線段![]() 從點
從點![]() 運動到點
運動到點![]() ,點
,點![]() 隨之運動,求點
隨之運動,求點![]() 的運動路徑的長度.
的運動路徑的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com