(2008•來賓)現分別有甲、乙兩種原料320千克和220千克,計劃用這兩種原料生產A、B兩種產品共50件.已知生產一件A產品需用甲原料7千克,乙原料3千克,可獲利潤600元;生產一件B產品需用甲原料4千克,乙原料8千克,可獲利潤1100元.設生產A、B兩種產品獲總利潤為y(元),其中A產品的生產件數為x(件).
(1)試寫出y與x之間的函數關系式;
(2)根據原料情況安排A、B兩種產品的生產件數,共有幾種生產方案?并結合(1)說明哪一種生產方案獲得的總利潤最大,最大利潤是多少?
【答案】
分析:(1)總利潤=A產品利潤+B產品利潤;
(2)兩個關系式為:A產品的數量×7+B產品數量×4≤320,A產品數量×3+B產品數量×8≤220,可解得x的取值范圍,x取整,可得到方案的個數,再根據(1)中的函數式可得到x為多少,獲利最大.
解答:解:(1)y=600x+(50-x)×1100=-500x+55000;
(2)
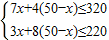
,
解得36≤x≤40,
∵x為整數,
∴x可取36,37,38,39,40;
∴共有5種生產方案,
由(1)得y隨x的增大而減少,
∴x=36時,y最大為37000.
答:生產A36件,B14件,利潤最大為37000元.
點評:考查一次函數與一元一次不等式的應用;得到相應的利潤及總原料的關系式是解決本題的關鍵.

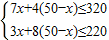 ,
,

 小學教材完全解讀系列答案
小學教材完全解讀系列答案