Question

已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=8，則此等腰梯形的面積為    ．

Answer 1

【答案】分析：根據等腰梯形的性質，作高，構造矩形和直角三角形，再利用已知條件進行解答．
解答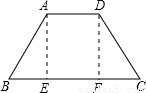：解：如圖，作AE⊥BC，DF⊥BC，垂足為E、F，
∵AD∥BC，
∴∠AEF=∠EFD=∠FDA=∠DAE=90°，
∴四邊形AEFD是矩形，
∵AD=2，
∴EF=2，
∵梯形ABCD是等腰梯形，
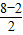
∴BE=FC==3，
又∵∠B=60°，
∴AE=3，
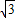
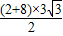
∴梯形的面積為：=15
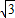點評：本題是考查梯形等腰梯形性質的典型題目，同時考查了梯形面積的計算．