
 ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4( ab),由此推導出一個重要的結論,a2+b2=c2,這個重要的結論就是著名的“勾股定理”.這種根據圖形可以極簡單地直觀推論或驗證數學規律和公式的方法,簡稱“無字證明”.
ab),由此推導出一個重要的結論,a2+b2=c2,這個重要的結論就是著名的“勾股定理”.這種根據圖形可以極簡單地直觀推論或驗證數學規律和公式的方法,簡稱“無字證明”.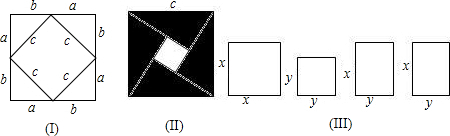
 解:(1)大正方形的面積為:c2,中間空白部分正方形面積為:(b-a)2;
解:(1)大正方形的面積為:c2,中間空白部分正方形面積為:(b-a)2; ab;
ab; ab=b2-2ab+a2+2ab=a2+b2;
ab=b2-2ab+a2+2ab=a2+b2;


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com