
【題目】有一個邊長為m+3的正方形,先將這個正方形兩鄰邊長分別增加1和減少1,得到的長方形①的面積為S1.
(1)試探究該正方形的面積S與S1的差是否是一個常數,如果是,求出這個常數;如果不是,說明理由;
(2)再將這個正方形兩鄰邊長分別增加4和減少2,得到的長方形②的面積為S2.
①試比較S1,S2的大小;
②當m為正整數時,若某個圖形的面積介于S1,S2之間(不包括S1,S2)且面積為整數,這樣的整數值有且只有16個,求m的值.
【答案】(1)解:S與S1的差是是一個常數,S與S1的差是1;(2)①當-2m+1﹥0,即-1﹤m﹤![]() 時,
時,![]() ﹥
﹥![]() ;當-2m+1﹤0,即m﹥
;當-2m+1﹤0,即m﹥![]() 時,
時,![]() ﹤
﹤![]() ;當-2m+1= 0,即m =
;當-2m+1= 0,即m =![]() 時,
時,![]() =
= ![]() ;②m= 9.
;②m= 9.
【解析】
(1)根據完全平方公式和多項式乘以多項式,計算即可得到答案.
(2)①先計算S1,S2,則有![]() ,再分情況討論,即可得到答案.
,再分情況討論,即可得到答案.
②根據題意列不等式16<![]() ≤17,即可得到答案.
≤17,即可得到答案.
(1)解:S與S1的差是是一個常數,
∵![]() ,
,![]()
∴![]() ,∴S與S1的差是1.
,∴S與S1的差是1.
(2)∵![]()
![]()
∴![]() ,∴當-2m+1﹥0,即-1﹤m﹤
,∴當-2m+1﹥0,即-1﹤m﹤![]() 時,
時,![]() ﹥
﹥![]() ;
;
當-2m+1﹤0,即m﹥![]() 時,
時,![]() ﹤
﹤![]() ;當-2m+1= 0,即m =
;當-2m+1= 0,即m =![]() 時,
時,![]() =
= ![]() ;
;
②由①得,S1﹣S2=-2m+1,∴![]() ,∵m為正整數,∴
,∵m為正整數,∴![]() ,∵一個圖形的面積介于S1,S2之間(不包括S1,S2)且面積為整數,整數值有且只有16個,∴16<
,∵一個圖形的面積介于S1,S2之間(不包括S1,S2)且面積為整數,整數值有且只有16個,∴16<![]() ≤17,∴
≤17,∴![]() <m≤9,∵m為正整數,∴m= 9.
<m≤9,∵m為正整數,∴m= 9.


科目:初中數學 來源: 題型:
【題目】某花圃銷售一批名貴花卉,平均每天可售出20盆,每盆盈利40元,為了增加盈利并盡快減少庫存,花圃決定采取適當的降價措施,經調查發現,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)若花圃平均每天要盈利1200元,每盆花卉應降價多少元?
(2)每盆花卉降低多少元時,花圃平均每天盈利最多,是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等邊△ABC中,
(1)如圖1,若D為線段BC中點,線段AD關于直線AB的對稱線段為線段AE,連接DE,求∠BDE的度數;
(2)若點D為線段BC上一動點(不與B,C重合),連接AD并將線段AD繞點D逆時針旋轉60°得到線段DE,連接BE.
①根據題意在圖2中補全圖形;
②小玉通過觀察、驗證,提出猜測:在點D運動的過程中,恒有CD=BE.請幫助小玉證明CD=BE.
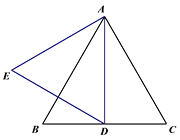
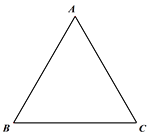
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() ,
,![]() ,以
,以![]() 為圓心,任意長為半徑畫弧,分別交
為圓心,任意長為半徑畫弧,分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,再分別以
,再分別以![]() ,
,![]() ,為圓心,大于
,為圓心,大于![]() 長為半徑畫弧,兩弧交于點
長為半徑畫弧,兩弧交于點![]() ,作弧線
,作弧線![]() ,交
,交![]() 于點
于點![]() .已知
.已知![]() ,
,![]() ,則
,則![]() 的長為( )
的長為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,C分別在x軸,y軸上,四邊形ABCO為矩形,AB=16,AC=20,點D與點A關于y軸對稱,點E、F分別是線段AD、AC上的動點(點E不與點A、D重合),且∠CEF=∠ACB.
(1)直接寫出BC的長是 ,點D的坐標是 ;
(2)證明:△AEF與△DCE相似;
(3)當△EFC為等腰三角形時,求點E的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節三天假期的某一天,小明全家上午8時自駕小汽車從家里出發,到某著名旅游景點游玩.該小汽車離家的距離S(千米)與時間t(小時)的關系如圖所示.
(1)在這個過程中,自變量是 ,因變量是 .
(2)景點離小明家多遠?
(3)小明一家在景點游玩的時間是多少小時?
(4)小明到家的時間是幾點?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,一次函數y=kx+b(k,b都是常數,且k≠0)的圖象經過點(1,0)和(0,2).
(1)當﹣2<x≤3時,求y的取值范圍;
(2)已知點P(m,n)在該函數的圖象上,且m﹣n=4,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】浠水縣商場某柜臺銷售每臺進價分別為160元、120元的A、B兩種型號的電風扇,下表是近兩周的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 3臺 | 4臺 | 1200元 |
第二周 | 5臺 | 6臺 | 1900元 |
(進價、售價均保持不變,利潤=銷售收入﹣進貨成本)
(1)求A、B兩種型號的電風扇的銷售單價;
(2)若商場準備用不多于7500元的金額再采購這兩種型號的電風扇共50臺,求A種型號的電風扇最多能采購多少臺?
(3)在(2)的條件下,商場銷售完這50臺電風扇能否實現利潤超過1850元的目標?若能,請給出相應的采購方案;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com