
在平面直角坐標(biāo)系中,二次函數(shù)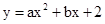 的圖象與x軸交于A(-3,0),B(1,0)兩點(diǎn),與y軸交于點(diǎn)C.
的圖象與x軸交于A(-3,0),B(1,0)兩點(diǎn),與y軸交于點(diǎn)C.
(1)求這個(gè)二次函數(shù)的關(guān)系解析式;
(2)點(diǎn)P是直線AC上方的拋物線上一動(dòng)點(diǎn),是否存在點(diǎn)P,使△ACP的面積最大?若存在,求出點(diǎn)P的坐標(biāo);若不存在,說明理由;
考生注意:下面的(3)、(4)、(5)題為三選一的選做題,即只能選做其中一個(gè)題目,多答時(shí)只按作答的首題評分,切記啊!
(3)在平面直角坐標(biāo)系中,是否存在點(diǎn)Q,使△BCQ是以BC為腰的等腰直角三角形?若存在,直接寫出點(diǎn)Q的坐標(biāo);若不存在,說明理由;
(4)點(diǎn)Q是直線AC上方的拋物線上一動(dòng)點(diǎn),過點(diǎn)Q作QE垂直于x軸,垂足為E.是否存在點(diǎn)Q,使以點(diǎn)B、Q、E為頂點(diǎn)的三角形與△AOC相似?若存在,直接寫出點(diǎn)Q的坐標(biāo);若不存在,說明理由;
(5)點(diǎn)M為拋物線上一動(dòng)點(diǎn),在x軸上是否存在點(diǎn)Q,使以A、C、M、Q為頂點(diǎn)的四邊形是平行四邊形?若存在,直接寫出點(diǎn)Q的坐標(biāo);若不存在,說明理由.
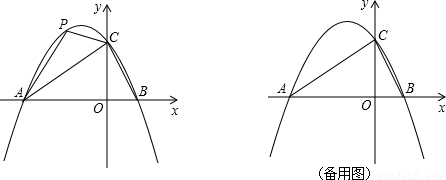
(1) (2)存在點(diǎn)
(2)存在點(diǎn)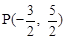 ,使△ACP的面積最大(3)存在。點(diǎn)
,使△ACP的面積最大(3)存在。點(diǎn)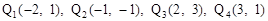 (4)存在。點(diǎn)
(4)存在。點(diǎn)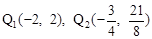 。(5)點(diǎn)
。(5)點(diǎn)
【解析】解:(1)由拋物線 過A(-3,0),B(1,0),則
過A(-3,0),B(1,0),則
 ,解得
,解得 。
。
∴二次函數(shù)的關(guān)系解析式為 。
。
(2)設(shè)點(diǎn)P坐標(biāo)為(m,n),則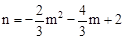 。
。
連接PO,作PM⊥x軸于M,PN⊥y軸于N。
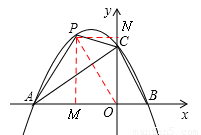
PM =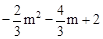 ,
, 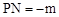 ,AO=3。
,AO=3。
當(dāng)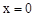 時(shí),
時(shí),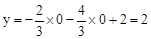 ,所以O(shè)C=2。
,所以O(shè)C=2。
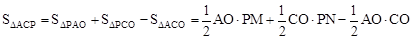 111
111
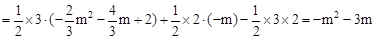
∵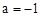 <0,∴函數(shù)
<0,∴函數(shù)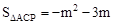 有最大值,當(dāng)
有最大值,當(dāng)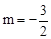 時(shí),
時(shí),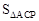 有最大值。
有最大值。
此時(shí) 。
。
∴存在點(diǎn)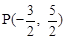 ,使△ACP的面積最大。
,使△ACP的面積最大。
(3)存在。點(diǎn)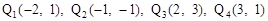 。
。
(4)存在。點(diǎn)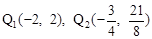 。
。
(5)點(diǎn)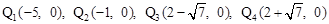 。
。
(1)將點(diǎn)A、B的坐標(biāo)代入 即可求得a、b,從而得到二次函數(shù)的關(guān)系解析式。
即可求得a、b,從而得到二次函數(shù)的關(guān)系解析式。
(2)設(shè)點(diǎn)P坐標(biāo)為(m,n),則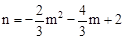 。連接PO,作PM⊥x軸于M,PN⊥y軸于N,根據(jù)
。連接PO,作PM⊥x軸于M,PN⊥y軸于N,根據(jù) 求出S關(guān)于m的二次函數(shù),根據(jù)二次函數(shù)最值求法即可求解。
求出S關(guān)于m的二次函數(shù),根據(jù)二次函數(shù)最值求法即可求解。
(3)分BQ為斜邊和CQ為斜邊兩種情況討論即可。
(4)分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三種情況討論即可。
(5)分AC是邊和對角線兩種情況討論即可。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 坐標(biāo)原點(diǎn).A、B兩點(diǎn)的橫坐標(biāo)分別是方程x2-4x-12=0的兩根,且cos∠DAB=
坐標(biāo)原點(diǎn).A、B兩點(diǎn)的橫坐標(biāo)分別是方程x2-4x-12=0的兩根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 18、在平面直角坐標(biāo)系中,把一個(gè)圖形先繞著原點(diǎn)順時(shí)針旋轉(zhuǎn)的角度為θ,再以原點(diǎn)為位似中心,相似比為k得到一個(gè)新的圖形,我們把這個(gè)過程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點(diǎn)O順時(shí)針旋轉(zhuǎn)的角度為90°,再以原點(diǎn)為位似中心,相似比為2得到一個(gè)新的圖形△A1B1C1,可以把這個(gè)過程記為【90°,2】變換.
18、在平面直角坐標(biāo)系中,把一個(gè)圖形先繞著原點(diǎn)順時(shí)針旋轉(zhuǎn)的角度為θ,再以原點(diǎn)為位似中心,相似比為k得到一個(gè)新的圖形,我們把這個(gè)過程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點(diǎn)O順時(shí)針旋轉(zhuǎn)的角度為90°,再以原點(diǎn)為位似中心,相似比為2得到一個(gè)新的圖形△A1B1C1,可以把這個(gè)過程記為【90°,2】變換.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com