
【題目】(本小題滿分9分)如圖,在矩形ABCD中,E是AB邊的中點,沿EC對折矩形ABCD,使B點落在點P處,折痕為EC,連結AP并延長AP交CD于F點,
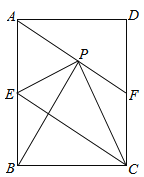
(1)求證:四邊形AECF為平行四邊形;
(2)若△AEP是等邊三角形,連結BP,求證:△APB≌△EPC;
(3)若矩形ABCD的邊AB=6,BC=4,求△CPF的面積.
【答案】(1)證明見試題解析;(2)證明見試題解析;(3)![]() .
.
【解析】
試題(1)由折疊的性質得到BE=PE,EC⊥PB,根據E為AB中點,得到AE=PE,利用等角對等邊得到兩對角相等,利用外角性質得到∠AEP=2∠EPB,設∠EPB=x,則∠AEP=2x,表示出∠APE,由∠APE+∠EPB得到∠APB為90°,進而得到AF與EC平行,再由AE與FC平行,利用兩對邊平行的四邊形為平行四邊形即可得證;
(2)根據等邊三角形性質,得到△AEP三條邊相等,三內角相等,再由折疊的性質及鄰補角定義得到一對角相等,根據同角的余角相等得到一對角相等,再由AP=EB,利用AAS即可得證;
(3)過P作PM⊥CD,在Rt△EBC中,利用勾股定理求出EC,利用面積求出BQ,再根據BP=2BQ求出BP,在Rt△ABP中,利用勾股定理求出AP,根據AF-AP求出PF,由PM與AD平行,得到△PMF與△ADF相似,由相似得比例求出PM,再由FC=AE=3,求出△CPF面積即可.
試題解析:(1)由折疊得到BE=PE,EC⊥PB,∵E為AB的中點,∴AE=EB,即AE=PE,∴∠EBP=∠EPB,∠EAP=∠EPA,∵∠AEP為△EBP的外角,∴∠AEP=2∠EPB,設∠EPB=x,則∠AEP=2x,∠APE=![]() =90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四邊形AECF為平行四邊形;
=90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四邊形AECF為平行四邊形;
(2)∵△AEP為等邊三角形,∴∠BAP=∠AEP=60°,AP=AE=EP=EB,∵∠PEC=∠BEC,∴∠PEC=∠BEC=60°,∵∠BAP+∠ABP=90°,∠ABP+∠BEQ=90°,∴∠BAP=∠BEQ,在△ABP和△EBC中,∵∠APB=∠EBC=90°,∠BAP=∠BEQ,AP=EB,∴△ABP≌△EBC(AAS),∵△EBC≌△EPC,∴△ABP≌△EPC;
(3)過P作PM⊥DC,交DC于點M,在Rt△EBC中,EB=3,BC=4,根據勾股定理得:EC=![]() =5,∵S△EBC=
=5,∵S△EBC=![]() EBBC=
EBBC=![]() ECBQ,∴BQ=
ECBQ,∴BQ=![]() =
=![]() ,由折疊得:BP=2BQ=
,由折疊得:BP=2BQ=![]() ,在Rt△ABP中,AB=6,BP=
,在Rt△ABP中,AB=6,BP=![]() ,根據勾股定理得:AP=
,根據勾股定理得:AP=![]() =
=![]() ,∵四邊形AECF為平行四邊形,∴AF=EC=5,FC=AE=3,∴PF=
,∵四邊形AECF為平行四邊形,∴AF=EC=5,FC=AE=3,∴PF=![]() =
=![]() ,∵PM∥AD,∴
,∵PM∥AD,∴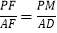 ,即
,即![]() ,解得:PM=
,解得:PM=![]() ,則S△PFC=
,則S△PFC=![]() FCPM=
FCPM=![]() =
=![]() .
.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
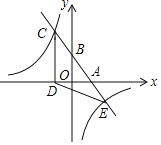
【題目】如圖,一次函數y=kx+b(k、b為常數,k≠0)的圖象與x軸、y軸分別交于A、B兩點,且與反比例函數y=![]() (n為常數,且n≠0)的圖象在第二象限交于點C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(n為常數,且n≠0)的圖象在第二象限交于點C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(1)求一次函數與反比例函數的解析式;
(2)記兩函數圖象的另一個交點為E,求△CDE的面積;
(3)直接寫出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中華文明,源遠流長:中華漢字,寓意深廣,為了傳承優秀傳統文化,某校團委組織了一次全校3000名學生參加的“漢字聽寫”大賽,賽后發現所有參賽學生的成績均不低于50分.為了更好地了解本次大賽的成績分布情況,隨機抽取了其中200名學生的成績(成績x取整數,總分100分)作為樣本進行整理,得到下列不完整的統計圖表:
成績x/分 | 頻數 | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
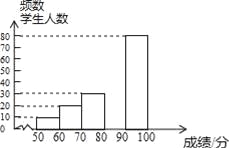
請根據所給信息,解答下列問題:
(1)a=______,b=______;
(2)請補全頻數分布直方圖;
(3)這次比賽成績的中位數會落在_____________分數段;
(4)若成績在90分以上(包括90分)的為“優”等,則該校參加這次比賽的3000名學生中成績“優”等約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了增強學生體質,決定開設以下體育課外活動項目:A:籃球 B:乒乓球C:羽毛球 D:足球,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,請回答下列問題:


(1)這次被調查的學生共有 人;
(2)請你將條形統計圖(2)補充完整;
(3)在平時的乒乓球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加乒乓球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】江南農場收割小麥,已知1臺大型收割機和3臺小型收割機1小時可以收割小麥1.4公頃,2臺大型收割機和5臺小型收割機1小時可以收割小麥2.5公頃.
(1)每臺大型收割機和每臺小型收割機1小時收割小麥各多少公頃?
(2)大型收割機每小時費用為300元,小型收割機每小時費用為200元,兩種型號的收割機一共有10臺,要求2小時完成8公頃小麥的收割任務,且總費用不超過5400元,有幾種方案?請指出費用最低的一種方案,并求出相應的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
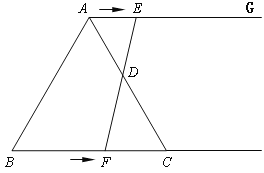
【題目】如圖,在等邊三角形ABC中,BC=6cm. 射線AG//BC,點E從點A出發沿射線AG以1cm/s的速度運動,同時點F從點B出發沿射線BC以2cm/s的速度運動,設運動時間為t(s).
(1)連接EF,當EF經過AC邊的中點D時,求證:△ADE≌△CDF;
(2)填空:當t為_________s時,四邊形ACFE是菱形;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O為菱形ABCD對角線上一點,以點O為圓心,OA長為半徑的⊙O與BC相切于點M.
(1)求證:CD與⊙O相切;
(2)若菱形ABCD的邊長為2,∠ABC=60°,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,一次函數y=﹣2x+8的圖象與x軸,y軸分別交于點A,點C,過點A作AB⊥x軸,垂足為點A,過點C作CB⊥y軸,垂足為點C,兩條垂線相交于點B.

(1)線段AB,BC,AC的長分別為AB= ,BC= ,AC= ;
(2)折疊圖1中的△ABC,使點A與點C重合,再將折疊后的圖形展開,折痕DE交AB于點D,交AC于點E,連接CD,如圖2.
請從下列A、B兩題中任選一題作答,我選擇 題.
A:①求線段AD的長;
②在y軸上,是否存在點P,使得△APD為等腰三角形?若存在,請直接寫出符合條件的所有點P的坐標;若不存在,請說明理由.
B:①求線段DE的長;
②在坐標平面內,是否存在點P(除點B外),使得以點A,P,C為頂點的三角形與△ABC全等?若存在,請直接寫出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com