
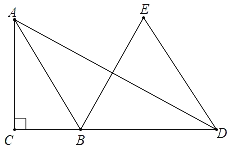
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延長線上一點,以BD為邊向上作等邊三角形EBD,連接AD,若AD=11,且∠ABE=2∠ADE,則tan∠ADE的值為_____.
,D是CB延長線上一點,以BD為邊向上作等邊三角形EBD,連接AD,若AD=11,且∠ABE=2∠ADE,則tan∠ADE的值為_____.
【答案】![]() .
.
【解析】
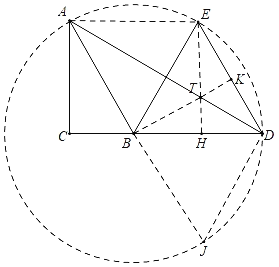
如圖,在線段DA上取一點T,使得DT=TE,連接ET,BT,AE,延長BT交DE于K,作TH⊥BD于H.想辦法證明∠EAB=![]() ∠EBD,推出點A在B為圓心,BE為半徑的⊙B上,延長AB交⊙B于J,連接DJ.解直角三角形求出TK,DK即可解決問題.
∠EBD,推出點A在B為圓心,BE為半徑的⊙B上,延長AB交⊙B于J,連接DJ.解直角三角形求出TK,DK即可解決問題.
解:如圖,在線段DA上取一點T,使得DT=TE,連接ET,BT,AE,延長BT交DE于K,作TH⊥BD于H.
∵△BDE是等邊三角形,
∴BE=BD,∠EBD=60°,
∵TE=TD,BT=BT,
∴△BTE≌△BTD(SSS),
∴∠EBT=∠DBT=30°,
∵BE=BD,
∴BK⊥DE,EK=DK,
∵TE=TD,
∴∠TED=∠TDE,
∴∠ATE=∠TED+∠TDE=2∠TDE,
∵∠ABE=2∠ADE,
∴∠ABE=∠ATE,
∴A,B,T,E四點共圓,
∴∠EAT=∠EBT=30°,
∴∠EAB=![]() ∠EBD,
∠EBD,
∴點A在B為圓心,BE為半徑的⊙B上,延長AB交⊙B于J,連接DJ.
∵AJ是直徑,
∴∠ADJ=90°,
∴DJ=![]()
∴tan∠DAJ=![]() ,
,
∵BA=BD,
∴∠BDA=∠BAD,
∴tan∠BDA=![]() ,
,
∵TH⊥DH,
∴![]() =
=![]() ,設TH=
,設TH=![]() k,則DH=11k,
k,則DH=11k,
在Rt△BHT中,BH=![]() =9k,
=9k,
∴BD=BH+DH=20k=![]() ,
,
∴k=![]() ,
,
∴BT=2TH=![]() ,
,
∵BK=BDcos30°=![]() ,
,
∴TK=BK﹣BT=![]() ,
,
∵DK=![]() ,
,
∴tan∠ADE=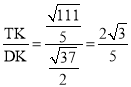 .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
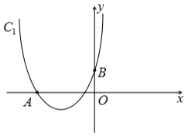
【題目】如圖,拋物線![]() :
:![]() (
(![]() ,
,![]() 是常數)經過
是常數)經過![]() 、
、![]() 兩點.
兩點.
(1)求![]() ,
,![]() 的值;
的值;
(2)向右平移拋物線![]() ,使它經過點
,使它經過點![]() ,得拋物線
,得拋物線![]() ,
,![]() 與
與![]() 軸的一個交點為
軸的一個交點為![]() ,且在另一個交點的左側.
,且在另一個交點的左側.
①求拋物線![]() 的表達式;
的表達式;
②![]() 是點
是點![]() 關于拋物線
關于拋物線![]() 對稱軸的對稱點,
對稱軸的對稱點,![]() 是線段
是線段![]() 上一點,
上一點,![]() 軸,交拋物線
軸,交拋物線![]() 于點
于點![]() ,
,![]() 為垂足,設
為垂足,設![]() ,線段
,線段![]() 的長為
的長為![]() ,求
,求![]() 的值,使
的值,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
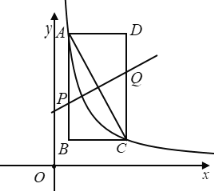
【題目】反比例函數y= ![]() (x>0) 的圖像經過矩形ABCD的頂點A、C,AC的垂直平分線分別交AB、CD于點P、Q;己知點B坐標為(1,2),矩形ABCD的面積為8.
(x>0) 的圖像經過矩形ABCD的頂點A、C,AC的垂直平分線分別交AB、CD于點P、Q;己知點B坐標為(1,2),矩形ABCD的面積為8.
(1)求k的值;
(2)求直線PQ的解析式;
(3)連接PC、AQ,判斷四邊形APC Q的形狀,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
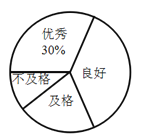
【題目】某校為了解七年級男生“跳繩”成績的情況,隨機選取該年級部分男生進行測試.以下是根據測試成績繪制的統計圖表的一部分.
成績等級 | 頻數(人) | 頻率 |
優秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根據以上信息,解答下列問題:
(1)被測試男生中,成績等級為“優秀”的男生人數占被測試男生總人數的百分比為________%,成績等級為“及格”的男生人數為________人;
(2)被測試男生的總人數為________人,成績等級為“不及格”的男生人數________人;
(3)若該校七年級共有570名男生,根據調查結果,估計該校七年級男生成績等級為“良好”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“只要人人都獻出一點愛,世界將變成美好的人間”,在新型肺炎疫情期間,全國人民萬眾一心,眾志成城,共克時艱.某社區積極發起“援鄂捐款”活動倡議,有2500名居民踴躍參與獻愛心.社區管理員隨機抽查了部分居民捐款情況,統計圖如圖:

(1)計算本次共抽查居民人數,并將條形圖補充完整;
(2)根據統計情況,請估計該社區捐款20元以上(含20元)的居民有多少人?
(3)該社區有1名男管理員和3名女管理員,現要從中隨機挑選2名管理員參與“社區防控”宣講活動,請用列表法或樹狀圖法求出恰好選到“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
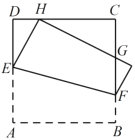
【題目】如圖,將正方形![]() 折疊,使頂點
折疊,使頂點![]() 與
與![]() 邊上的一點
邊上的一點![]() 重合(
重合(![]() 不與端點
不與端點![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,邊
,邊![]() 折疊后與邊
折疊后與邊![]() 交于點
交于點![]() ,設正方形
,設正方形![]() 的周長為
的周長為![]() ,
,![]() 的周長為
的周長為![]() ,則
,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
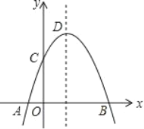
【題目】如圖,拋物線y=﹣x2+2x+m+1交x軸于點A(a,0)和B(b,0),交y軸于點C,拋物線的頂點為D,下列四個命題:
①當x>0時,y>0;
②若a=﹣1,則b=3;
③拋物線上有兩點P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,則y1>y2;
④點C關于拋物線對稱軸的對稱點為E,點G,F分別在x軸和y軸上,當m=2時,四邊形EDFG周長的最小值為6![]() .
.
其中真命題的序號是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
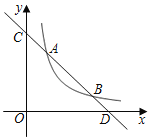
【題目】如圖,已知一次函數y1=kx+b與反比例函數y2=![]() (x>0)的圖象分別交于點A(2,4)和點B(4,n),與坐標軸分別交于點C和點D.
(x>0)的圖象分別交于點A(2,4)和點B(4,n),與坐標軸分別交于點C和點D.
(1)求反比例函數和一次函數的解析式;
(2)求y1<y2時,自變量x的取值范圍;
(3)若點P是x軸上一動點,當△ABP為直角三角形時,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com