
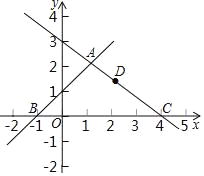
【題目】如圖,在平面直角坐標系可中,直線y=x+1與y=﹣![]() x+3交于點A,分別交x軸于點B和點C,點D是直線AC上的一個動點.
x+3交于點A,分別交x軸于點B和點C,點D是直線AC上的一個動點.
(1)求點A,B,C的坐標;
(2)在直線AB上是否存在點E使得四邊形EODA為平行四邊形?存在的話直接寫出![]() 的值,不存在請說明理由;
的值,不存在請說明理由;
(3)當△CBD為等腰三角形時直接寫出D坐標.
【答案】(1)A(![]() ,
,![]() ),B(﹣1,0),C(4,0);(2)存在,
),B(﹣1,0),C(4,0);(2)存在,![]() =
=![]() ;(3)點D的坐標為(﹣
;(3)點D的坐標為(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
【解析】
(1)將y=x+1與y=﹣![]() x+3聯立求得方程組的解可得到點A的坐標,然后將y=0代入函數解析式求得對應的x的值可得到點B、C的橫坐標;
x+3聯立求得方程組的解可得到點A的坐標,然后將y=0代入函數解析式求得對應的x的值可得到點B、C的橫坐標;
(2)當OE∥AD時,存在四邊形EODA為平行四邊形,然后依據平行線分線段成比例定理可得到![]() =
=![]() ;
;
(3)當DB=DC時,點D在BC的垂直平分線上可先求得點D的橫坐標;即AC與y軸的交點為F,可求得CF=BC=F,當點D與點F重合或點D與點F關于點C對稱時,三角形BCD為等腰三角形,當BD=BC時,設點D的坐標為(x,﹣![]() x+3),依據兩點間的距離公式可知:(x+1)2+(﹣
x+3),依據兩點間的距離公式可知:(x+1)2+(﹣![]() x+3)2=25,從而可求得點D的橫坐標.
x+3)2=25,從而可求得點D的橫坐標.
(1)將y=x+1與y=﹣![]() x+3聯立得:
x+3聯立得: ,
,
解得:x=![]() ,y=
,y=![]() ,
,
∴A(![]() ,
,![]() ).
).
把y=0代入y=x+1得:x+1=0,解得x=﹣1,
∴B(﹣1,0).
把y=0代入y=﹣![]() x+3得:﹣
x+3得:﹣![]() x+3=0,解得:x=4,
x+3=0,解得:x=4,
∴C(4,0).
(2)如圖,存在點E使EODA為平行四邊形.

∵EO∥AC,
∴![]() =
=![]() =
=![]() .
.
(3)當點BD=DC時,點D在BC的垂直平分線上,則點D的橫坐標為![]() ,
,
將x=![]() 代入直線AC的解析式得:y=
代入直線AC的解析式得:y=![]() ,
,
∴此時點D的坐標為(![]() ,
,![]() ).
).
如圖所示:
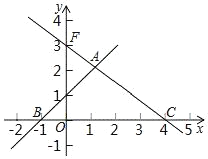
FC=![]() =5,
=5,
∴BC=CF,
∴當點D與點F重合時,△BCD為等腰三角形,
∴此時點D的坐標為(0,3);
當點D與點F關于點C對稱時,CD=CB,
∴此時點D的坐標為(8,﹣3),
當BD=DC時,設點D的坐標為(x,﹣![]() x+3),
x+3),
依據兩點間的距離公式可知:(x+1)2+(﹣![]() x+3)2=25,
x+3)2=25,
解得x=4(舍去)或x=﹣![]() ,
,
將x=﹣![]() 代入y=﹣
代入y=﹣![]() x+3得y=
x+3得y=![]() ,
,
∴此時點D的坐標為(﹣![]() ,
,![]() ).
).
綜上所述點D的坐標為(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AC=3,BC=4,分別以AB、AC、BC為邊在AB同側作正方形ABEF、ACPQ、BCMN,四塊陰影部分的面積分別為S1、S2、S3、S4.則S1-S2+S3+S4等于( )
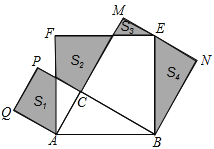
A. 4B. 6C. 8D. 10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)已知a2+b2=10,a+b=4,求a﹣b的值;
(2)關于x的代數式(ax﹣3)(2x+1)﹣4x2+m化簡后不含有x2項和常數項,且an+mn=1,求2n3﹣9n2+8n+2019的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,是由幾個小立方塊所搭幾何體的俯視圈,小立方塊中的數字表示在該位置小立方塊的個數.

(1)請在網格內畫出從正面和從左面看到的這個幾何體的形狀圖.
(2)如圖,是小明用9個棱長為1![]() 的小立方塊積木搭成的幾何體的俯視圖,小立方塊中的數字表示在該位置小立方塊的個數,他請小亮用盡可能少的同樣大小的立方塊在旁邊再搭建一個幾何體,使小亮所搭建的幾何體恰好可以和小明所搭建的幾何體拼成一個大的正方體(即拼大正方體時將其中一個幾何體翻轉,且假定組成每個幾何體的立方塊粘合在一起),則:
的小立方塊積木搭成的幾何體的俯視圖,小立方塊中的數字表示在該位置小立方塊的個數,他請小亮用盡可能少的同樣大小的立方塊在旁邊再搭建一個幾何體,使小亮所搭建的幾何體恰好可以和小明所搭建的幾何體拼成一個大的正方體(即拼大正方體時將其中一個幾何體翻轉,且假定組成每個幾何體的立方塊粘合在一起),則:
①小亮至少還需要 個小正方體;
②上面①中小亮所搭幾何體的表面積為 ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是邊長為4的正方形,E為AB的中點,將△ADE繞點D沿逆時針方向旋轉后得到△DCF,連接EF,則EF的長為( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數![]() 的圖象經過點A(1,4)和點B.過點A作AC⊥x軸,垂足為點C,過點B作BD⊥y軸,垂足為點D,連結AB、BC、DC、DA.點B的橫坐標為a(a>1)
的圖象經過點A(1,4)和點B.過點A作AC⊥x軸,垂足為點C,過點B作BD⊥y軸,垂足為點D,連結AB、BC、DC、DA.點B的橫坐標為a(a>1)
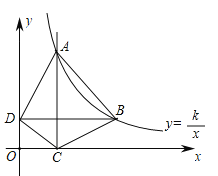
(1)求k的值
(2)若△ABD的面積為4;
①求點B的坐標,
②在平面內存在點E,使得以點A、B、C、E為頂點的四邊形是平行四邊形,直接寫出符合條件的所有點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并解答其后的問題:
我國古代南宋數學家秦九韶在其所著書《數學九章》中,利用“三斜求積術”十分巧妙的解決了已知三角形三邊求其面積的問題,這與西方著名的“海倫公式”是完全等價的.我們也稱這個公式為“海倫秦九韶公式”,該公式是:設△ABC中,∠A、∠B、∠C所對的邊分別為a、b、c,△ABC的面積為S=![]() .
.
(1)(舉例應用)已知△ABC中,∠A、∠B、∠C所對的邊分別為a、b、c,且a=4,b=5,c=7,則△ABC的面積為 ;
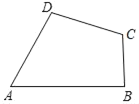
(2)(實際應用)有一塊四邊形的草地如圖所示,現測得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求該塊草地的面積.
m,∠A=60°,求該塊草地的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
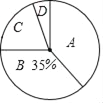
【題目】2017年4月15日至5月15日,某市約8萬名初三畢業生參加了中考體育測試,為了了解今年初三畢業生的體育成績,從某校隨機抽取了60名學生的測試成績,根據測試評分標準,將他們的得分按優秀、良好、及格、不及格(分別用A、B、C、D表示)四個等級進行統計,并繪制成下面的扇形圖和統計表:
等級 | 成績(分) | 頻數(人數) | 頻率 |
A | 27~30 | 24 | 0.4 |
B | 23~26 | m | x |
C | 19~22 | n | y |
D | 18及18以下 | 3 | 0.05 |
合計 | 60 | 1.00 |
請你根據以上圖表提供的信息,解答下列問題:
(1)m= ,n= ,x= ,y= ;
(2)在扇形圖中,B等級所對應的圓心角是 度;
(3)請你估計某市這8萬名初三畢業生成績等級達到優秀和良好的大約有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成績均為A,現決定從這四名同學中選兩名參加學校組織的體育活動,直接寫出恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com