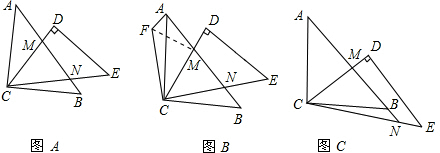
解:(1)△CMF≌△CMN.
理由∵△BCN繞點C逆時針旋轉(zhuǎn)90°得到△ACF,
∴CF=CN,∠ACF=∠BCN,
∵∠DCE=45°,
∴∠ACM+∠BCN=45°,
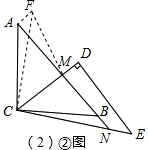
∴∠ACM+∠ACF=45°,
即∠MCF=45°,
∴∠MCF=∠MCN,
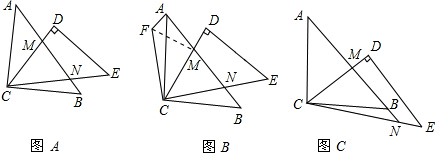
在△CMF和△CMN中,
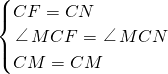
,
∴△CMF≌△CMN(SAS);
(2)①∵△CMF≌△CMN,
∴FM=MN,
∵∠CAF=∠B=45°,
∴∠FAM=∠CAF+∠BAC=45°+45°=90°,
∴AM
2+AF
2=FM
2,
∴AM
2+BN
2=MN
2;
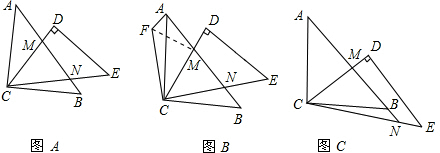
②如圖,把△BCN繞點C逆時針旋轉(zhuǎn)90°得到△ACF,
則AF=BN,CF=CN,∠BCN=∠ACF,
∵∠MCF=∠ACB-∠MCB-∠ACF=90°-(45°-∠BCN)-∠ACF=45°+∠BCN-∠ACF=45°,
∴∠MCF=∠MCN,
在△CMF和△CMN中,
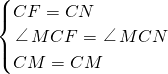
,
∴△CMF≌△CMN(SAS),
∴FM=MN,
∵∠ABC=45°,
∴∠CAF=∠CBN=135°,
又∵∠BAC=45°,
∴∠FAM=∠CAF-∠BAC=135°-45°=90°,
∴AM
2+AF
2=FM
2,
∴AM
2+BN
2=MN
2.
分析:(1)根據(jù)旋轉(zhuǎn)的性質(zhì)可得CF=CN,∠ACF=∠BCN,再求出∠ACM+∠BCN=45°,從而求出∠MCF=45°,然后利用“邊角邊”可以證明出△CMF和△CMN全等;
(2)①根據(jù)全等三角形對應(yīng)邊相等可得FM=MN,再根據(jù)旋轉(zhuǎn)的性質(zhì)可得AF=BN,∠CAF=∠B=45°,從而求出∠BAF=90°,再利用勾股定理列式即可得解;
②把△BCN繞點C逆時針旋轉(zhuǎn)90°得到△ACF,根據(jù)旋轉(zhuǎn)的性質(zhì)可得AF=BN,CF=CN,∠BCN=∠ACF,再求出∠MCF=∠MCN,然后利用“邊角邊”證明△CMF和△CMN全等,根據(jù)全等三角形對應(yīng)邊相等可得MF=MN,然后利用勾股定理列式即可得解.
點評:本題考查了旋轉(zhuǎn)的性質(zhì),全等三角形的判定與性質(zhì),等腰直角三角形的性質(zhì),此類題目根據(jù)相同的思路確定出全等的三角形,然后找出條件是解題的關(guān)鍵.


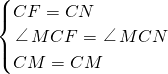 ,
,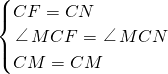 ,
,

 巧學(xué)巧練系列答案
巧學(xué)巧練系列答案