
【題目】如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(![]() ,0)、(0,4),拋物線
,0)、(0,4),拋物線![]() 經過B點,且頂點在直線
經過B點,且頂點在直線![]() 上.
上.
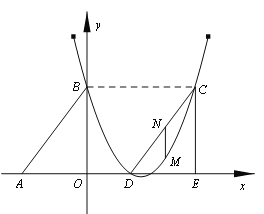
(1)求拋物線對應的函數關系式;
(2)若△DCE是由△ABO沿x軸向右平移得到的,當四邊形ABCD是菱形時,試判斷點C和點D是否在該拋物線上,并說明理由;
(3)若M點是CD所在直線下方該拋物線上的一個動點,過點M作MN平行于y軸交CD于點N.設點M的橫坐標為t,MN的長度為l.求l與t之間的函數關系式,并求l取最大值時,點M的坐標.
【答案】(1)![]()
(2)在,理由略
(3)M的坐標為(![]() ,
, ![]() )
)
【解析】試題分析:(1)已知了拋物線上A、B點的坐標以及拋物線的對稱軸方程,可用待定系數法求出拋物線的解析式.
(2)首先求出AB的長,將A、B的坐標向右平移AB個單位,即可得出C、D的坐標,再代入拋物線的解析式中進行驗證即可.
(3)根據C、D的坐標,易求得直線CD的解析式;那么線段MN的長實際是直線BC與拋物線的函數值的差,可將x=t代入兩個函數的解析式中,得出的兩函數值的差即為l的表達式,由此可求出l、t的函數關系式,根據所得函數的性質即可求出l取最大值時,點M的坐標.
解:(1)∵拋物線y=![]() +bx+c的頂點在直線x=上,
+bx+c的頂點在直線x=上,
∴可設所求拋物線對應的函數關系式為y=![]() +m
+m
∵點B(0,4)在此拋物線上,
∴4=×![]() +m
+m
∴m=﹣
∴所求函數關系式為:y=![]() ﹣=
﹣=![]() ﹣
﹣![]() x+4
x+4
(2)在Rt△ABO中,OA=3,OB=4,
∴AB=![]() =5
=5
∵四邊形ABCD是菱形
∴BC=CD=DA=AB=5
∴C、D兩點的坐標分別是(5,4)、(2,0);
當x=5時,y=×52﹣![]() ×5+4=4
×5+4=4
當x=2時,y=×22﹣![]() ×2+4=0
×2+4=0
∴點C和點D在所求拋物線上;
(3)設直線CD對應的函數關系式為y=kx+b′,
則![]() ;
;
解得:![]() ;
;
∴y=x﹣
∵MN∥y軸,M點的橫坐標為t,
∴N點的橫坐標也為t;
則yM=![]() ﹣
﹣![]() t+4,yN=t﹣,
t+4,yN=t﹣,
∴l=yN﹣yM=t﹣﹣(![]() ﹣
﹣![]() t+4)=﹣
t+4)=﹣![]() +
+![]() t﹣
t﹣![]() =﹣
=﹣![]() +
+
∵﹣<0,
∴當t=時,l最大=,yM=![]() ﹣
﹣![]() t+4=.
t+4=.
此時點M的坐標為(,).


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,P、Q分別是BC、AC上的點,作PR⊥AB,PS⊥AC,垂足分別為R、S,若AQ=PQ,PR=PS,則下列四個結論:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中結論正確的序號為( ) 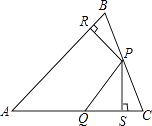
A.①②③
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數填在相應的括號里:
﹣8,0.275, ![]() ,0,﹣1.04,﹣(﹣3),﹣
,0,﹣1.04,﹣(﹣3),﹣ ![]() ,|﹣2|
,|﹣2|
正數集合{…}
負整數集合{…}
分數集合{…}
負數集合{…}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一件羽絨服先按成本提高50%標價,再以8折(標價的80%)出售,結果獲利250元.若設這件羽絨服的成本是x元,根據題意,可得到的方程是( )
A.x(1+50%)×80%=x﹣250
B.x(1+50%)×80%=x+250
C.(1+50%x)×80%=x﹣250
D.(1+50%x)×80%=250﹣x
查看答案和解析>>
科目:初中數學 來源: 題型:
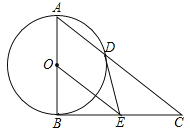
【題目】如圖,在△ABC中,∠ABC=90°,以AB的中點O為圓心,OA為半徑的圓交AC于點D,E是BC的中點,連接DE,OE.
(1)判斷DE與⊙O的位置關系,并說明理由;
(2)求證:BC2=2CDOE;
(3)若![]() ,求OE的長.
,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解學生家長對孩子使用手機的態度情況,隨機抽取部分學生家長進行問卷調查,發出問卷150份,每位學生家長1份,每份問卷僅表明一種態度,將回收的問卷進行整理(假設回收的問卷都有效),并繪制了如圖所示的兩幅不完整的統計圖. 根據以上信息解答下列問題:
(1)回收的問卷數為份,“嚴加干涉”部分對應扇形的圓心角度數;
(2)把條形統計圖補充完整;
(3)若將“從來不管”和“稍加詢問”視為“管理不嚴”,已知全校共1200名學生,請估計該校對孩子使用手機“管理不嚴”的家長有多少人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com