
【解題思路】如圖:延長MA交CB于點E. CD=DN+CN=DN+ME.
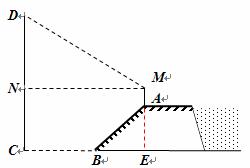
在![]() 中,背水坡AB的坡比
中,背水坡AB的坡比![]() 可知
可知![]() ,
,
得![]() 。又AB=20 m,所以AE=
。又AB=20 m,所以AE= ![]() ×20=10m,BE=20×
×20=10m,BE=20×![]() =
= ![]() m
m
所以NC=ME=MA=AE=1.7+10=11.7m
![]() 中,∠AMN=30°,MN=CE=CB+BE=(30+
中,∠AMN=30°,MN=CE=CB+BE=(30+![]() )m
)m
DN= ![]()
所以旗桿高度CD=DN+CN=DN+ME=11.7+![]() =
= ![]() ≈36.0m
≈36.0m
【答案】 ![]() ≈36.0
≈36.0
在圓內接四邊形ABCD中,CD為∠BCA外角的平分線,F為弧AD上一點,BC=AF,延長DF與BA的延長線交于E.
⑴求證△ABD為等腰三角形.
⑵求證AC•AF=DF•FE
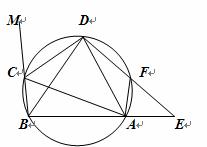
【解題思路】(1)利用同角的補角相等,同弧所對的圓周角相等,等量代換;
(2)證等積式就要找三角形相似,發現AC、AF、FE所在的三角形,且利用等弧對等弦,同圓中等弦對等弧,發現DF可以被DC替換,進而求解。
【答案】⑴由圓的性質知∠MCD=∠DAB、∠DCA=∠DBA,而∠MCD=∠DCA,所以∠DBA=∠DAB,故△ABD為等腰三角形.
⑵∵∠DBA=∠DAB
∴弧AD=弧BD
又∵BC=AF
∴弧BC=弧AF、∠CDB=∠FDA
∴弧CD=弧DF
∴CD=DF
再由“圓的內接四邊形外角等于它的內對角”知
∠AFE=∠DBA=∠DCA①,∠FAE=∠BDE
∴∠CDA=∠CDB+∠BDA=∠FDA+∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE
∴AC:FE=CD:AF
∴AC•AF= CD •FE
而CD=DF,
∴AC•AF=DF•FE


科目:初中數學 來源: 題型:閱讀理解

查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:2013屆江蘇省南京市鼓樓區中考二模數學試卷(帶解析) 題型:解答題
【提出問題】
如圖①,在梯形ABCD中,AD//BC,AC、BD交于點E,∠BEC=n°,若AD=a,BC=b,則梯形ABCD的面積最大是多少?
【探究過程】
小明提出:可以從特殊情況開始探究,如圖②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,則梯形ABCD的面積最大是多少?
如圖③,過點D做DE//AC交BC的延長線于點E,那么梯形ABCD的面積就等于△DBE的面積,求梯形ABCD的面積最大值就是求△DBE的面積最大值.如果設AC=x,BD=y,那么S△DBE=xy.
以下是幾位同學的對話:
A同學:因為y= ,所以S△DBE=x
,所以S△DBE=x ,求這個函數的最大值即可.
,求這個函數的最大值即可.
B同學:我們知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同學:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我們先將所有滿足BE=10的直角△DBE都找出來,然后在其中尋找高最大的△DBE即可.


(1)請選擇A同學或者B同學的方法,完成解題過程.
(2)請幫C同學在圖③中畫出所有滿足條件的點D,并標出使△DBE面積最大的點D1.(保留作圖痕跡,可適當說明畫圖過程)
【解決問題】
根據對特殊情況的探究經驗,請在圖①中畫出面積最大的梯形ABCD的頂點D1,并直接寫出梯形ABCD面積的最大值.
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省南京市鼓樓區中考二模數學試卷(解析版) 題型:解答題
【提出問題】
如圖①,在梯形ABCD中,AD//BC,AC、BD交于點E,∠BEC=n°,若AD=a,BC=b,則梯形ABCD的面積最大是多少?
【探究過程】
小明提出:可以從特殊情況開始探究,如圖②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,則梯形ABCD的面積最大是多少?
如圖③,過點D做DE//AC交BC的延長線于點E,那么梯形ABCD的面積就等于△DBE的面積,求梯形ABCD的面積最大值就是求△DBE的面積最大值.如果設AC=x,BD=y,那么S△DBE=xy.
以下是幾位同學的對話:
A同學:因為y= ,所以S△DBE=x
,所以S△DBE=x ,求這個函數的最大值即可.
,求這個函數的最大值即可.
B同學:我們知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同學:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我們先將所有滿足BE=10的直角△DBE都找出來,然后在其中尋找高最大的△DBE即可.

(1)請選擇A同學或者B同學的方法,完成解題過程.
(2)請幫C同學在圖③中畫出所有滿足條件的點D,并標出使△DBE面積最大的點D1.(保留作圖痕跡,可適當說明畫圖過程)
【解決問題】
根據對特殊情況的探究經驗,請在圖①中畫出面積最大的梯形ABCD的頂點D1,并直接寫出梯形ABCD面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com