
(1)證明:∵△BCD為等邊三角形,
∴∠3=∠4=60°,DC=DB,
∵△ABD繞著點D按順時針方向旋轉60°后得到△ECD,
∴∠5=∠1+∠4=∠1+60°,
∴∠2+∠3+∠5=∠2+∠1+120°,
∵∠BAC=120°,
∴∠1+∠2=180°-∠BAC=60°,
∴∠2+∠3+∠5=60°+120°=180°,
∴點A、C、E在一條直線上;
(2)解:∵點A、C、E在一條直線上,
而△ABD繞著點D按順時針方向旋轉60°后得到△ECD,
∴∠ADE=60°,DA=DE,
∴△ADE為等邊三角形,
∴∠DAE=60°,
∴∠BAD=∠BAC-∠DAE=120°-60°=60°,;
(3)解:∵點A、C、E在一條直線上,
∴AE=AC+CE,
∵△ABD繞著點D按順時針方向旋轉60°后得到△ECD,
∴CE=AB,
∴AE=AC+AB=2+3=5,
∵△ADE為等邊三角形,
∴AD=AE=5.
分析:(1)根據等邊三角形的性質由△BCD為等邊三角形得到∠3=∠4=60°,DC=DB,再根據旋轉的性質得到∠5=∠1+∠4=∠1+60°,則∠2+∠3+∠5=∠2+∠1+120°,再根據三角形內角和定理得到
∠1+∠2=180°-∠BAC=60°,于是∠2+∠3+∠5=60°+120°=180°,即可得到點A、C、E在一條直線上;
(2)由于點A、C、E在一條直線上,△ABD繞著點D按順時針方向旋轉60°后得到△ECD,則∠ADE=60°,DA=DE,得到△ADE為等邊三角形,則∠DAE=60°,然后利用∠BAD=∠BAC-∠DAE計算即可;
(3)由于點A、C、E在一條直線上,則AE=AC+CE,根據旋轉的性質得到CE=AB,則AE=AC+AB=2+3=5,而△ADE為等邊三角形,則AD=AE=5.
點評:本題考查了旋轉的性質:旋轉前后兩圖形全等;對應點到旋轉中心的距離相等;對應點與旋轉中心的連線段的夾角等于旋轉角.也考查了等邊三角形的判定與性質.

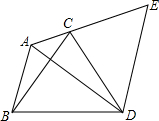 已知:如圖,在△ABC中,∠BAC=120°,以BC為邊向形外作等邊△BCD,把△ABD繞著點D按順時針方向旋轉60°后得到△ECD,若AB=3,AC=2.
已知:如圖,在△ABC中,∠BAC=120°,以BC為邊向形外作等邊△BCD,把△ABD繞著點D按順時針方向旋轉60°后得到△ECD,若AB=3,AC=2. (1)證明:∵△BCD為等邊三角形,
(1)證明:∵△BCD為等邊三角形,

 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案 (2013•啟東市一模)已知,如圖,在Rt△ABC中,∠C=90°,∠BAC的角平分線AD交BC邊于D.
(2013•啟東市一模)已知,如圖,在Rt△ABC中,∠C=90°,∠BAC的角平分線AD交BC邊于D. 已知:如圖,在△ABC中,∠C=120°,邊AC的垂直平分線DE與AC、AB分別交于點D和點E.
已知:如圖,在△ABC中,∠C=120°,邊AC的垂直平分線DE與AC、AB分別交于點D和點E.