【題目】如圖1，
，
，
是鄭州市二七區三個垃圾存放點，點，分別位于點的正北和正東方向，
米．八位環衛工人分別測得的
長度如下表：
甲 | 丁 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他們又調查了各點的垃圾量，并繪制了下列間不完整的統計圖2．
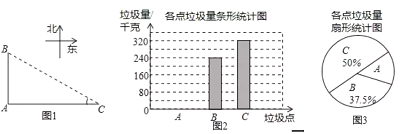
（1）表中的中位數是 、眾數是 ；
（2）求表中長度的平均數
；
（3）求處的垃圾量，并將圖2補充完整；
（4）用（2）中的作為的長度，要將處的垃圾沿道路
都運到處，已知運送1千克垃圾每米的費用為0.005元，求運垃圾所需的費用．
【答案】（1）81米，84米；（2）80米；（3）80千克，圖詳見解析；（4）運垃圾所需的費用為
元．
【解析】
（1）根據中位數和眾數的定義即可得；
（2）根據平均數的計算公式
即可得；
（3）先根據C處垃圾量的扇形統計圖和條形統計圖信息求出三處垃圾總量，再減去B、C兩處的垃圾量可得A處的垃圾量，然后補全條形統計圖即可；
（4）先利用勾股定理求出AB的長，再根據“運送1千克垃圾每米的費用為
元”列出式子求解即可得．
（1）由眾數的定義得：眾數是84米
由中位數的定義，先將表中的數據從小到大進行順序為
，則中位數是
（米）
故答案為：81米，84米；
（2）由平均數的計算公式得：
（米）
答：表中
長度的平均數
為80米；
（3）A、B、C三處垃圾總量為
（千克）
則
處的垃圾總量是：
（千克）
補全條形統計圖如下：
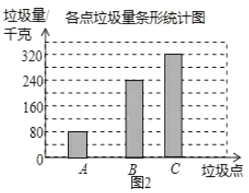
（4）在直角
中，
（米）
∵運送1千克垃圾每米的費用為元
∴運垃圾所需的費用為
（元）
答：運垃圾所需的費用為元．
科目：初中數學 來源： 題型：
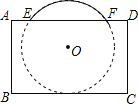
【題目】把球放在長方體紙盒內，球的一部分露出盒外，其主視圖如圖．⊙O與矩形ABCD的邊BC，AD分別相切和相交（E，F是交點），已知EF=CD=8，則⊙O的半徑為
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，∠BAC=90°，點D是邊BC上的動點，連接AD，點C關于直線AD的對稱點為點E，射線BE與射線AD交于點F.
（1）在圖1中，依題意補全圖形；
（2）記
（
），求
的大小；（用含
的式子表示）
（3）若△ACE是等邊三角形，猜想EF和BC的數量關系，并證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
對于任意正實數a、b，
∵
，
當且僅當
時，等號成立．
結論：在
均為正實數)中，若
為定值
則
當且僅當時，a+b有最小值
．
拓展：對于任意正實數
，都有
當且僅當
時，等號成立．
在(a、b、c均為正實數)中，若
為定值
，則
當且僅當時，
有最小值
例如：
則
，當且僅當
，即
時等號成立．
又如：若求
的最小值時，因為
當且僅當
，即時等號成立，故當時，有最小值
．
根據上述材料，解答下列問題：
（1）若a為正數，則當a=______時，代數式
取得最小值，最小值為_____；
（2）已知函數
與函數
，求函數
的最小值及此時
的值；
（3）我國某大型空載機的一次空載運輸成本包含三部分：一是基本運輸費用，共8100元；二是飛行耗油，每一百公里1200元；三是飛行報耗費用，飛行報耗費用與路程(單位：百公里)的平方成正比，比例系數為0.04，設該空載機的運輸路程為百公里，則該空載機平均每一百公里的運輸成本
最低為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，已知拋物線
（
、
為常數）的頂點為
，等腰直角三角形
的頂點
的坐標為
，
的坐標為
，直角頂點
在第四象限．
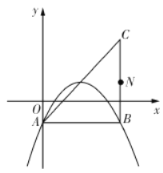
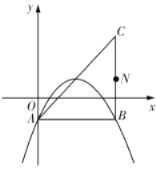
（1）如圖，若該拋物線經過、兩點，求該拋物線的函數表達式；
（2）平移（1）中的拋物線，使頂點在直線
上滑動，且與交于另一點
．
①若點
在直線下方，且為平移前（1）中的拋物線上的點，當以、、三點為頂點的三角形是等腰直角三角形時，求出所有符合條件的點的坐標；
②取
的中點
，連接
，
，求
的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
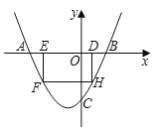
【題目】如圖，拋物線
與 x 軸交于點 A、B，與 y 軸交于點 C，且 OC＝2OB， 點 D 為線段 OB 上一動點(不與點 B 重合)，過點 D 作矩形 DEFH，點 H、F 在拋物線上，點 E 在 x 軸 上．
（1）求拋物線的解析式；
（2）當矩形 DEFH 的周長最大時，求矩形 DEFH 的面積；
（3）在（2）的條件下，矩形 DEFH 不動，將拋物線沿著 x 軸向左平移 m 個單位，拋物線與矩形 DEFH的邊交于點 M、N，連接 M、N．若 MN 恰好平分矩形 DEFH 的面積，求 m 的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD內接于⊙O，∠BAD =90°，AC是對角線．點E在BC的延長線上，且∠CED =∠BAC．
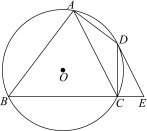
（1）判斷DE與⊙O的位置關系，并說明理由；
（2）BA與CD的延長線交于點F，若DE∥AC，AB=4，AD =2，求AF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=x2+2ax-3與x軸交于A、B(1，0)兩點(點A在點B的左側)，與y軸交于點C，將拋物線沿y軸平移m(m＞0)個單位，當平移后的拋物線與線段OA有且只有一個交點時，則m的取值范圍是_______________
查看答案和解析>>
科目：初中數學 來源： 題型：
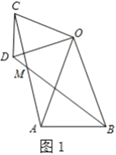
【題目】（1）問題發現：如圖1，在
和
中，
，連接
交于點
．求證：
；并直接寫出
______．
（2）類比探究：如圖2，在和中，
，連接
交
的延長線于點．請判斷
的值及
的度數．
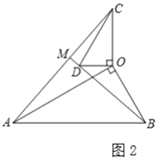
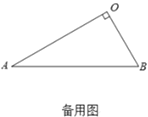
（3）拓展延伸：在（2）的條件下，將繞點
在平面內旋轉，所在直線交于點．若
，請直接寫出當點
與點重合時的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
