
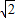 a,分別計算OF的最大、最小值,求△DBF的面積的最大值、最小值.
a,分別計算OF的最大、最小值,求△DBF的面積的最大值、最小值.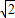 b,
b,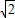 b,
b, DF•AB=
DF•AB= (a-
(a-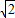 b)a=
b)a= a2-
a2-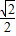 ab;
ab; BA•AD=
BA•AD= a2,
a2, a2;
a2;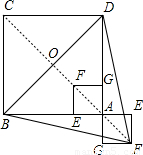
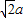
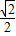 a(
a(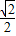 a+
a+ b)=
b)= a2+ab,
a2+ab,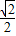 a(
a(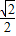 a-
a-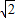 b)=
b)= a2-ab.
a2-ab.

科目:初中數學 來源: 題型:
 23、已知:如圖,在正方形ABCD中,點E、F分別在BC和CD上,AE=AF.
23、已知:如圖,在正方形ABCD中,點E、F分別在BC和CD上,AE=AF.查看答案和解析>>
科目:初中數學 來源: 題型:
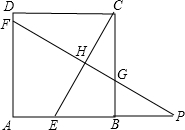 、CE、CB于點F、H、G,交AB的延長線于點P.
、CE、CB于點F、H、G,交AB的延長線于點P.| 7 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 24、已知,如圖,在正方形ABCD中,點E、F分別在AB上和AD的延長線上,且BE=DF,連接EF,G為EF的中點.
24、已知,如圖,在正方形ABCD中,點E、F分別在AB上和AD的延長線上,且BE=DF,連接EF,G為EF的中點.查看答案和解析>>
科目:初中數學 來源: 題型:
 已知:如圖,在正方形ABCD中,P為對角線AC上的一動點,PE⊥AB于E,PF⊥BC于F,過點P作DP的垂線交BC于點G,DG交AC于點Q.下列說法:①EF=DP;②EF⊥DP;③
已知:如圖,在正方形ABCD中,P為對角線AC上的一動點,PE⊥AB于E,PF⊥BC于F,過點P作DP的垂線交BC于點G,DG交AC于點Q.下列說法:①EF=DP;②EF⊥DP;③| DG |
| DP |
| 2 |
| AP2+QC2 |
| PQ2 |
| 2 |
| A、①②③④ | B、①②③ |
| C、①②④ | D、①③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:
 F,BF與邊CD交于點G,連接EG.設CE=x.
F,BF與邊CD交于點G,連接EG.設CE=x.| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com