
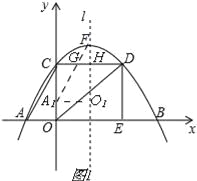
【題目】如圖,已知拋物線y=ax2+bx+c經過點A(﹣3,0),B(9,0)和C(0,4).CD垂直于y軸,交拋物線于點D,DE垂直與x軸,垂足為E,l是拋物線的對稱軸,點F是拋物線的頂點.
(1)求出二次函數的表達式以及點D的坐標;
(2)若Rt△AOC沿x軸向右平移到其直角邊OC與對稱軸l重合,再沿對稱軸l向上平移到點C與點F重合,得到Rt△A1O1F,求此時Rt△A1O1F與矩形OCDE重疊部分的圖形的面積;
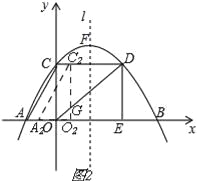
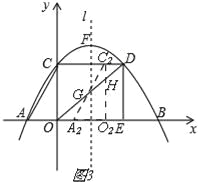
(3)若Rt△AOC沿x軸向右平移t個單位長度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2與Rt△OED重疊部分的圖形面積記為S,求S與t之間的函數表達式,并寫出自變量t的取值范圍.

【答案】(1)D(6,4);y=﹣![]() x2+
x2+![]() x+4;(2)
x+4;(2)![]() ;(3)當0<t≤3時,S=
;(3)當0<t≤3時,S=![]() t2,當3<t≤6時,S=
t2,當3<t≤6時,S=![]() t2﹣3t+12
t2﹣3t+12
【解析】試題分析:(1)用待定系數法求拋物線解析式;(2)由GH∥A1O1,求出GH=1,再求出FH,S重疊部分=S△A1O1F﹣S△FGH計算即可;(3)分兩種情況①直接用面積公式計算,②用面積差求出即可.
試題解析:(1)∵拋物線y=ax2+bx+c經過點A(﹣3,0),B(9,0)和C(0,4).
∴設拋物線的解析式為y=a(x+3)(x﹣9), ∵C(0,4)在拋物線上, ∴4=﹣27a,
∴a=﹣![]() , ∴設拋物線的解析式為y=﹣
, ∴設拋物線的解析式為y=﹣![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣![]() x2+
x2+![]() x+4,
x+4,
∵CD垂直于y軸,C(0,4) ∴﹣![]() x2+
x2+![]() x+4=4, ∴x=6, ∵D(6,4),
x+4=4, ∴x=6, ∵D(6,4),
(2)如圖1, ∵點F是拋物線y=﹣![]() x2+
x2+![]() x+4的頂點,∴F(3,
x+4的頂點,∴F(3,![]() ), ∴FH=
), ∴FH=![]() ,
,
∵GH∥A1O1, ∴![]() , ∴
, ∴![]() , ∴GH=1,
, ∴GH=1,
∵Rt△A1O1F與矩形OCDE重疊部分是梯形A1O1HG,
∴S重疊部分=S△A1O1F﹣S△FGH=![]()
![]() A1O1×O1F﹣
A1O1×O1F﹣![]()
![]() GH×FH=
GH×FH=![]() ×3×4﹣
×3×4﹣![]() ×1×
×1×![]() =
=![]() .
.
(3)①當0<t≤3時,如圖2, ∵C2O2∥DE, ∴![]() , ∴
, ∴![]() , ∴O2G=
, ∴O2G=![]() t,
t,
∴S=S△OO2G=![]() OO2×O2G=
OO2×O2G=![]() t×
t×![]() t=
t=![]() t2,
t2,
②當3<t≤6時,如圖3, ∵C2H∥OC, ∴![]() , ∴
, ∴![]() , ∴C2H=
, ∴C2H=![]() (6﹣t),
(6﹣t),
∴S=S四邊形A2O2HG=S△A2O2C2﹣S△C2GH=![]() OA×OC﹣
OA×OC﹣![]() C2H×(t﹣3)=
C2H×(t﹣3)=![]() ×3×4﹣
×3×4﹣![]() ×
×![]() (6﹣t)(t﹣3)=
(6﹣t)(t﹣3)=![]() t2﹣3t+12
t2﹣3t+12
∴當0<t≤3時,S=![]() t2,當3<t≤6時,S=
t2,當3<t≤6時,S=![]() t2﹣3t+12.
t2﹣3t+12.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,以Rt△ABC的直角邊AB為直徑作⊙O,交斜邊AC于點D,點E為OB的中點,連接CE并延長交⊙O于點F,點F恰好落在弧AB的中點,連接AF并延長與CB的延長線相交于點G,連接OF.

(1)求證:OF=![]() BG;
BG;
(2)若AB=4,求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣(x﹣1)2+k上有點(﹣1,y1)、(0,y2)、(2,y3),那么有( )
A.y1<y2=y3
B.y1=y3<y2
C.y1=y3>y2
D.y1>y2=y3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知E,F分別為正方形ABCD的邊BC,CD上的點,AF,DE相交于點G,當E,F分別為邊BC,CD的中點時,有:①AF=DE;②AF⊥DE成立.
試探究下列問題:
(1)如圖1,若點E不是邊BC的中點,F不是邊CD的中點,且CE=DF,上述結論①,②是否仍然成立?(請直接回答“成立”或“不成立”),不需要證明)
(2)如圖2,若點E,F分別在CB的延長線和DC的延長線上,且CE=DF,此時,上述結論①,②是否仍然成立?若成立,請寫出證明過程,若不成立,請說明理由;
(3)如圖3,在(2)的基礎上,連接AE和EF,若點M,N,P,Q分別為AE,EF,FD,AD的中點,請判斷四邊形MNPQ是“矩形、菱形、正方形”中的哪一種,并證明你的結論.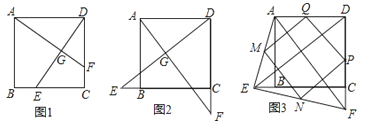
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“十一五”期間,中國減少二氧化碳排放1 460 000 000噸,贏得國際社會廣泛贊譽.將1 460 000 000用科學記數法表示為( )
A.146×107
B.1.46×107
C.1.46×109
D.1.46×1010
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標系中,平行于x軸的直線與拋物線y=ax(a>0)相交于A、B兩點.設點B的橫坐標為m(m>0).
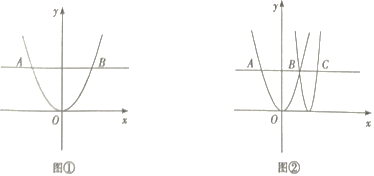
(1)求AB的長(用含m的代數式表示).
(2)如圖②,點C在直線AB上,點C的橫坐標為2m.若a=1,m=2,求頂點在x軸上且經過B、C兩點的拋物線的頂點坐標.
(3)點D在直線AB上,BD=2AB,過O、B、D三點的拋物線的頂點為P,其對應函數的二次項系數為a1.
①求![]() 的值.
的值.
②當m=2,△BPD為等腰直角三角形,直接寫出a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com