
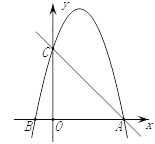
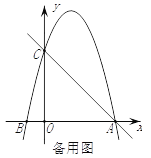
【題目】如圖,在平面直角坐標系中,已知點C(0,4),點A、B在x軸上,并且OA=OC=4OB,動點P在過A、B、C三點的拋物線上.
(1)求拋物線的函數表達式;
(2)在直線AC上方的拋物線上,是否存在點P,使得△PAC的面積最大?若存在,求出P點坐標及ΔPAC面積的最大值;若不存在,請說明理由.
(3)在x軸上是否存在點Q,使得△ACQ是等腰三角形?若存在,請直接寫出點Q的坐標;若不存在,請說明理由.
【答案】(1)y=x2+3x+4;(2)存在, 當P點坐標為(2,6)時,ΔPAC面積的最大值是8;(3)Q(0,0),(-4,0),![]() .
.
【解析】試題分析:(1)根據點C的坐標,即可求得OC的長,再求得點A、B的坐標,利用待定系數法即可求得函數的解析式;(2)存在,作PN⊥x軸交AC于N,先求得直線AC的解析式,設P(x,x2+3x+4),則N(x,-x+4),即可得PN=x2+4x ,根據三角形的面積公式可得S△PAC=![]() PN×4=-2(x-2)2+8 ,根據二次函數的性質可得當x=2時,ΔPAC面積的最大值為8,再求得點P的坐標即可;(3)根據勾股定理求得AC=4
PN×4=-2(x-2)2+8 ,根據二次函數的性質可得當x=2時,ΔPAC面積的最大值為8,再求得點P的坐標即可;(3)根據勾股定理求得AC=4![]() ,以A為頂點,以AC為腰時,可得AQ=4
,以A為頂點,以AC為腰時,可得AQ=4![]() ,此時可得Q的坐標為(4+4
,此時可得Q的坐標為(4+4![]() ,0)、(4-4
,0)、(4-4![]() ,0);以C為頂點,以AC為腰時,AC=AQ,因OC垂直于x軸,可得OA=OQ,此時點Q的坐標為(-4,0);以O為頂點,以AC為底邊時,此時點Q的坐標為(0,0),所以符合條件的點Q的坐標為:(0,0),(-4,0),
,0);以C為頂點,以AC為腰時,AC=AQ,因OC垂直于x軸,可得OA=OQ,此時點Q的坐標為(-4,0);以O為頂點,以AC為底邊時,此時點Q的坐標為(0,0),所以符合條件的點Q的坐標為:(0,0),(-4,0),![]() .
.
試題解析:
(1)∵C(0,4),∴OC=4.
∵OA=OC=4OB,∴OA=4,OB=1,
∴A(4,0),B(1,0),
設拋物線解析式:y=a(x+1)(x4),
∴4=4a,∴a=1.
∴y=x2+3x+4.
(2)存在.
作PN⊥x軸交AC于N,求得AC的解析式為y=-x+4 ,

設P(x,x2+3x+4),則N(x,-x+4),
得PN=(x2+3x+4)-(-x+4)=x2+4x ,
∴S△PAC=![]() PN×4=2PN=2(x2+4x)=-2(x-2)2+8 ,
PN×4=2PN=2(x2+4x)=-2(x-2)2+8 ,
當x=2時,ΔPAC面積的最大值為8,此時點P的坐標為(2,6).
∴P點坐標為(2,6)時,ΔPAC面積有最大值,最大面積是8 .
(3) 根據勾股定理求得AC=4![]() ,分三種情況:
,分三種情況:
①以A為頂點,以AC為腰時,可得AQ=4![]() ,此時可得Q的坐標為(4+4
,此時可得Q的坐標為(4+4![]() ,0)、(4-4
,0)、(4-4![]() ,0);
,0);
②以C為頂點,以AC為腰時,AC=AQ,因OC垂直于x軸,可得OA=OQ,此時點Q的坐標為(-4,0);
③以O為頂點,以AC為底邊時,此時點Q的坐標為(0,0),
綜上,符合條件的點Q的坐標為:(0,0),(-4,0),![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分c1與經過點A、D、B的拋物線的一部分c2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,﹣![]() ),點M是拋物線C2:y=mx2﹣2mx﹣3m(m<0)的頂點.
),點M是拋物線C2:y=mx2﹣2mx﹣3m(m<0)的頂點.
(1)求A、B兩點的坐標;
(2)“蛋線”在第四象限上是否存在一點P,使得△PBC的面積最大?若存在,求出△PBC面積的最大值;若不存在,請說明理由;
(3)當△BDM為直角三角形時,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有20筐白菜,以每筐30千克為標準,超過或不足的分別用正、負來表示,記錄如下:
與標準質量的差(單位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐數 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最輕的一筐要重多少千克?
(2)與標準質量比較,20筐白菜總計超過或不足多少千克?
(3)若白菜每千克售價2元,則出售這20筐白菜可賣多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線相交于點O,DE∥AC,CE∥BD.
(1)求證:四邊形OCED是菱形;
(2)若∠CAB=60,BC的長為![]() ,求四邊形OCED的周長
,求四邊形OCED的周長

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道:點A、B在數軸上分別表示有理數a、b,A、B兩點之間的距離表示為AB,在數軸上A、B兩點之間的距離AB=|a﹣b|.所以式子|x﹣3|的幾何意義是數軸上表示有理數3的點與表示有理數x的點之間的距離.
根據上述材料,直接下列問題答案:
(1)|5﹣(﹣2)|的值為_____;
(2)若|x﹣3|=1,則x的值為_____;
(3)若|x﹣3|=|x+1|,則x的值為_____;
(4)若|x﹣3|+|x+1|=7,則x的值為_____.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用棋子擺成的“上”字型圖案如圖所示現察此圖案的規律,并回答:
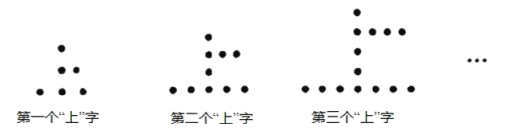
(1)依照此規律,第五個圖形中共有 個棋子,第八個圖形中共有 個棋子.
(2)第![]() (
(![]() 為正整數)個圖形中共有 個棋子.
為正整數)個圖形中共有 個棋子.
(3)根據(2)中的結論,第幾個圖形中有2022個棋子?
查看答案和解析>>
科目:初中數學 來源: 題型:
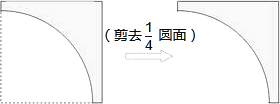
【題目】現在把一張正方形紙片按如圖方式剪去一個半徑為40![]() 厘米的圓面后得到如圖紙片,且該紙片所能剪出的最大圓形紙片剛好能與前面所剪的扇形紙片圍成一圓錐表面,則該正方形紙片的邊長約為( )厘米.(不計損耗、重疊,結果精確到1厘米,
厘米的圓面后得到如圖紙片,且該紙片所能剪出的最大圓形紙片剛好能與前面所剪的扇形紙片圍成一圓錐表面,則該正方形紙片的邊長約為( )厘米.(不計損耗、重疊,結果精確到1厘米,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
A. 64 B. 67 C. 70 D. 73
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列說法:
①若a+b+c=0,則b2﹣4ac>0;
②若方程兩根為﹣1和2,則2a+c=0;
③若方程ax2+c=0有兩個不相等的實根,則方程ax2+bx+c=0必有兩個不相等的實根;
④若b=2a+c,則方程有兩個不相等的實根.其中正確的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com