【題目】一名工人一天可以加工
個
零件，或者加工
個
零件，每一個零件和兩個零件可以組裝成一套零件，某車間共有
名工人，問應如何安排這些工人，使加工出來的零件剛好可以配套．
【答案】應安排
個工人加工
零件，安排
個工人加工
零件，才能使加工出來的零件剛好可以配套．
【解析】
設應安排x個工人加工A零件，安排（35-x）個工人加工B零件，才能使加工出來的零件剛好可以配套．根據加工的B零件的個數為A零件的2倍即可列出關于x的一元一次方程，解之即可得出結論.
解：設應安排x個工人加工A零件，安排（35-x）個工人加工B零件，才能使加工出來的零件剛好可以配套.
根據題意得：2×100x=150(35-x)，
解得：x=15，
∴35-x=35-15=20.
答：應安排15個工人加工A零件，安排20個工人加工B零件，才能使加工出來的零件剛好可以配套．
故答案為：應安排15個工人加工A零件，安排20個工人加工B零件，才能使加工出來的零件剛好可以配套．
習題精選系列答案科目：初中數學 來源： 題型：
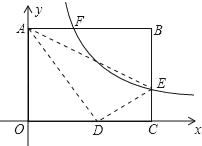
【題目】矩形OABC在平面直角坐標系中如圖，已知AB=10，BC=8，EB是C上一點，將△ABE沿AE折疊，點B剛好與OC邊上點D重合，過點E的反比例函數y=
（k＞0）與AB相交于點F，則線段AF的長為（ ）
A. 
B. 
C. 2 D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD的邊長為2，E是CD的中點，將△ADE繞點A按順時針方向旋轉后得到△ABF，則EF的長等于（ ）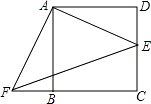 
A.3
B.
C.2 
D.3 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，BC是圓O的直徑，點A，F在圓O上，連接AB，BF． 
（1）如圖1，若點A、F把半圓三等分，連接OA，OA與BF交于點E．求證：E為OA的中點；
（2）如圖2，若點A為弧 
的中點，過點A作AD⊥BC，垂足為點D，AD與BF交于點G．求證：AG=BG．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，一次函數y=x+2的圖象交y軸于點A，交x軸于點B，點E在x軸的正半軸上，OE=8，點F在射線BA上，過點F作x軸的垂線，點D為垂足，OD=6．
（1）寫出點F的坐標 ；
（2）求證：∠ABO=45°；
（3）操作：將一塊足夠大的三角板的直角頂點放在線段BF的中點M處，一直角邊過點E，交FD于點C，另一直角邊與x軸相交于點N，如圖2，求點N的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】糧庫
天內進出庫的糧食噸數如下（“
”表示進庫，“
”表示出庫）：
，
，
，
，
，
.
（1）經過這天，庫里的糧食是增多了還是減少了？
（2）經過這天，倉庫管理員結算時發現庫里還存
噸糧食，那么天前庫里存糧多少噸？
（3）如果進出的裝卸費都是每噸
元，那么這天要付多少裝卸費？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=ax2+bx+c（a≠0）的對稱軸為x=1，且拋物線經過A（﹣1，0）、C（0，﹣3）兩點，與x軸交于另一點B．
（1）求這條拋物線所對應的函數關系式；
（2）在拋物線的對稱軸x=1上求一點M，使點M到點A的距離與到點C的距離之和最小，并求出此時點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店購進一批單價為16元的日用品，銷售一段時間后，為了獲得更多利潤，商店決定提高銷售價格．經試驗發現，若按每件20元的價格銷售時，每月能賣360件；若按每件25元的價格銷售時，每月能賣210件．假定每月銷售件數y（件）是價格x（元/件）的一次函數．
（1）試求y與x之間的關系式；
（2）在商品不積壓，且不考慮其它因素的條件下，問銷售價格定為多少時，才能使每月獲得最大利潤？每月的最大利潤是多少（總利潤=總收入﹣總成本）？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
