
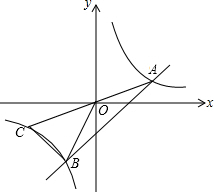
 如圖,直線y=x+b與雙曲線y=$\frac{k}{x}$交于A、B兩點,延長AO交雙曲線于C點,連接BC,且AB=2BC=4$\sqrt{2}$,則k=3.
如圖,直線y=x+b與雙曲線y=$\frac{k}{x}$交于A、B兩點,延長AO交雙曲線于C點,連接BC,且AB=2BC=4$\sqrt{2}$,則k=3. 分析 過O作OD⊥AB于點D,根據直線y=x+b中的k=1得到OD所在直線為y=-x,于是得到直線y=x+b關于此直線軸對稱,雙曲線y=k/x關于O中心對稱,求得AD=BD,AO=OC,根據平行線的性質得到BC⊥AC,設A(x,y)則B(-y,-x),根據勾股定理和兩點間的距離公式得到(2x)2+(2y)2=(2$\sqrt{10}$)2,(x+y)2+(y+x)2=(4$\sqrt{2}$)2求得點A 坐標為(1,3)于是得到結論.
解答 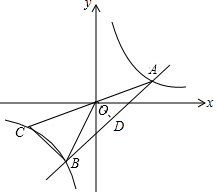 解:過O作OD⊥AB于點D,
解:過O作OD⊥AB于點D,
∴OD所在直線為y=-x,
∴直線y=x+b關于此直線軸對稱,雙曲線y=k/x關于O中心對稱,
∴AD=BD,AO=OC,
∴OD∥BC,
∴BC⊥AC,
設A(x,y)則B(-y,-x),
∵AB=2BC=4$\sqrt{2}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{10}$,
∴(2x)2+(2y)2=(2$\sqrt{10}$)2,(x+y)2+(y+x)2=(4$\sqrt{2}$)2
解得x=1,y=3
∴點A 坐標為(1,3)
∴k=3.
故答案為:3.
點評 本題考查了反比例函數與一次函數的交點坐標,勾股定理,兩點間的距離公式,正確的理解題意是解題的關鍵.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
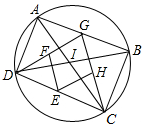 如圖,AC與BD是⊙I的直徑,AD=4,CD=10,點G是AB上一動點,點E、F、H分別是DC、DG、CG的中點.
如圖,AC與BD是⊙I的直徑,AD=4,CD=10,點G是AB上一動點,點E、F、H分別是DC、DG、CG的中點.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,兩個反比例函數y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限內的圖象依次是C1和C2,點P在C1上,矩形PCOD交C2于A、B兩點,OA的延長線交C1于點E,EF⊥x軸于F點,且圖中四邊形BOAP的面積為6,則EF:AC為$\sqrt{3}$.
如圖,兩個反比例函數y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限內的圖象依次是C1和C2,點P在C1上,矩形PCOD交C2于A、B兩點,OA的延長線交C1于點E,EF⊥x軸于F點,且圖中四邊形BOAP的面積為6,則EF:AC為$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在4×4的方格中有五個同樣大小的正方形如圖擺放,在其他空白方格中再任取一個涂上黑色,與其余五個正方形組成一個新圖形.
如圖,在4×4的方格中有五個同樣大小的正方形如圖擺放,在其他空白方格中再任取一個涂上黑色,與其余五個正方形組成一個新圖形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com