
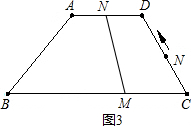
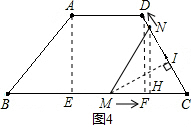
 ,∠B=45°,動點M從點B出發,沿線段BC以每秒1個單位長度的速度向終點C運動;動點N同時從C點出發,沿C→D→A,以同樣速度向終點A運動,當其中一個動點到達終點時,
,∠B=45°,動點M從點B出發,沿線段BC以每秒1個單位長度的速度向終點C運動;動點N同時從C點出發,沿C→D→A,以同樣速度向終點A運動,當其中一個動點到達終點時,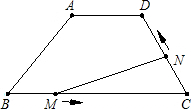 另一個動點也隨之停止運動.設運動的時間為t秒.
另一個動點也隨之停止運動.設運動的時間為t秒.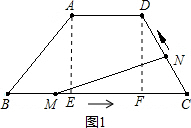 解:(1)如圖1,
解:(1)如圖1, ;
;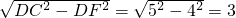 ;
;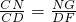 ,即
,即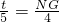 ;
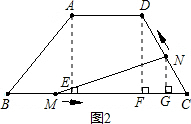
;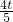 ;
;
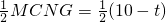
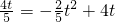 ;
;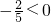 ,函數開口向下;
,函數開口向下;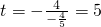 時,Smax=10;
時,Smax=10;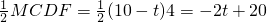 ;
;
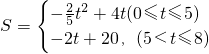 ,
,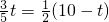 ,
,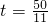 ;
;
 ,又
,又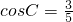 ,
,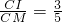 ,可得
,可得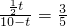 ,解得:
,解得: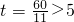 (舍去);
(舍去);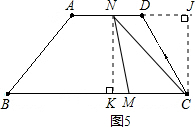
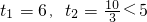 (舍去);
(舍去);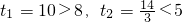 (舍去).
(舍去).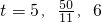 時,△MCN為等腰三角形.
時,△MCN為等腰三角形.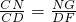 ,再利用當5≤t≤8時得出s與t的關系式求出即可;
,再利用當5≤t≤8時得出s與t的關系式求出即可;

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD為直徑的半圓O切AB于點E,這個梯形的面積為21cm2,周長為20cm,那么半圓O的半徑為( )
如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD為直徑的半圓O切AB于點E,這個梯形的面積為21cm2,周長為20cm,那么半圓O的半徑為( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com