
【題目】如圖,⊙E的圓心E(3,0),半徑為5,⊙E與y軸相交于A、B兩點(點A在點B的上方),與x軸的正半軸交于點C,直線l的解析式為y= ![]() x+4,與x軸相交于點D,以點C為頂點的拋物線過點B.
x+4,與x軸相交于點D,以點C為頂點的拋物線過點B.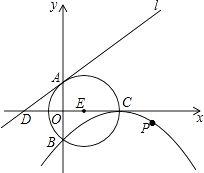
(1)求拋物線的解析式;
(2)判斷直線l與⊙E的位置關系,并說明理由;
(3)動點P在拋物線上,當點P到直線l的距離最小時.求出點P的坐標及最小距離.
【答案】
(1)
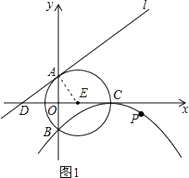
解:如圖1,連接AE,由已知得:AE=CE=5,OE=3,
在Rt△AOE中,由勾股定理得,OA= ![]() =
= ![]() =4,
=4,
∵OC⊥AB,
∴由垂徑定理得,OB=OA=4,
OC=OE+CE=3+5=8,
∴A(0,4),B(0,﹣4),C(8,0),
∵拋物線的頂點為C,
∴設拋物線的解析式為y=a(x﹣8)2,
將點B的坐標代入上解析的式,得64a=﹣4,故a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣8)2,
(x﹣8)2,
∴y=﹣ ![]() x2+x﹣4為所求拋物線的解析式
x2+x﹣4為所求拋物線的解析式
(2)
解:在直線l的解析式y= ![]() x+4中,令y=0,得
x+4中,令y=0,得 ![]() x+4=0,解得x=﹣
x+4=0,解得x=﹣ ![]() ,
,
∴點D的坐標為(﹣ ![]() ,0),
,0),
當x=0時,y=4,
∴點A在直線l上,
在Rt△AOE和Rt△DOA中,
∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA,
∴∠AEO=∠DAO,
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,即∠DAE=90°,因此,直線l與⊙E相切與A
(3)
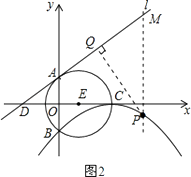
解:如圖2,過點P作直線l的垂線段PQ,垂足為Q,過點P作直線PM垂直于x軸,交直線l于點M.
設M(m, ![]() m+4),P(m,﹣
m+4),P(m,﹣ ![]() m2+m﹣4),則
m2+m﹣4),則
PM= ![]() m+4﹣(﹣
m+4﹣(﹣ ![]() m2+m﹣4)=
m2+m﹣4)= ![]() m2﹣
m2﹣ ![]() m+8=
m+8= ![]() (m﹣2)2+
(m﹣2)2+ ![]() ,
,
當m=2時,PM取得最小值 ![]() ,
,
此時,P(2,﹣ ![]() ),
),
對于△PQM,
∵PM⊥x軸,
∴∠QMP=∠DAO=∠AEO,
又∠PQM=90°,
∴△PQM的三個內角固定不變,
∴在動點P運動的過程中,△PQM的三邊的比例關系不變,
∴當PM取得最小值時,PQ也取得最小值,
PQ最小=PM最小sin∠QMP=PM最小sin∠AEO= ![]() ×
× ![]() =
= ![]() ,
,
∴當拋物線上的動點P的坐標為(2,﹣ ![]() )時,點P到直線l的距離最小,其最小距離為
)時,點P到直線l的距離最小,其最小距離為 ![]() .
.
【解析】(1)連接AE,由已知得:AE=CE=5,OE=3,利用勾股定理求出OA的長,結合垂徑定理求出OC的長,從而得到C點坐標,進而得到拋物線的解析式;(2)求出點D的坐標為(﹣ ![]() ,0),根據△AOE∽△DOA,求出∠DAE=90°,判斷出直線l與⊙E相切與A.(3)過點P作直線l的垂線段PQ,垂足為Q,過點P作直線PM垂直于x軸,交直線l于點M.設M(m,
,0),根據△AOE∽△DOA,求出∠DAE=90°,判斷出直線l與⊙E相切與A.(3)過點P作直線l的垂線段PQ,垂足為Q,過點P作直線PM垂直于x軸,交直線l于點M.設M(m, ![]() m+4),P(m,﹣
m+4),P(m,﹣ ![]() m2+m﹣4),得到PM=
m2+m﹣4),得到PM= ![]() m+4﹣(﹣
m+4﹣(﹣ ![]() m2+m﹣4)=
m2+m﹣4)= ![]() m2﹣
m2﹣ ![]() m+8=
m+8= ![]() (m﹣2)2+
(m﹣2)2+ ![]() ,根據△PQM的三個內角固定不變,得到PQ最小=PM最小sin∠QMP=PM最小sin∠AEO=
,根據△PQM的三個內角固定不變,得到PQ最小=PM最小sin∠QMP=PM最小sin∠AEO= ![]() ×
× ![]() =
= ![]() ,從而得到最小距離.
,從而得到最小距離.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)請在圖中,畫出△ABC向左平移6個單位長度后得到的△A1B1C1;
(Ⅱ)以點O為位似中心,將△ABC縮小為原來的 ![]() ,得到△A2B2C2 , 請在圖中y軸右側,畫出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 請在圖中y軸右側,畫出△A2B2C2 , 并求出∠A2C2B2的正弦值.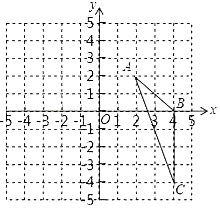
查看答案和解析>>
科目:初中數學 來源: 題型:
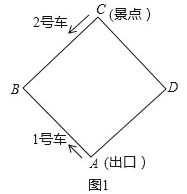
【題目】如圖,某景區內的環形路是邊長為1200米的正方形ABCD,現有1號、2號兩輛游覽車分別從出口A和景點C同時出發,1號車沿A→B→C→D→A路線、2號車沿C→B→A→D→C路線連續循環行駛,供游客隨時免費乘車(上、下車的時間忽略不計),兩車速度均為300米/分.
(1)如圖1,設行駛時間為t分(0≤t≤8)
①1號車、2號車離出口A的路程分別為_____米,_____米;(用含t的代數式表示)
②當兩車相距的路程是600米時,求t的值;
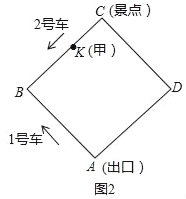
(2)如圖2,游客甲在BC上的一點K(不與點B、C重合)處候車,準備乘車到出口A,設CK=x米.
情況一:若他剛好錯過2號車,則他等候并搭乘即將到來的1號車;
情況二:若他剛好錯過1號車,則他等候并搭乘即將到來的2號車.
請判斷游客甲在哪種情況下乘車到出口A用時較多?(含候車時間)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,AE平分∠CAB交CD于點E.若∠C比∠AED小55°,則∠AED的度數為( )
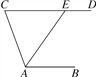
A. 55° B. 125° C. 135° D. 140°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級數學興趣小組經過市場調查,得到某種運動服每月的銷量與售價的相關信息如下表:
售價(元/件) | 100 | 110 | 120 | 130 | … |
月銷量(件) | 200 | 180 | 160 | 140 | … |
已知該運動服的進價為每件60元,設售價為x元.
(1)請用含x的式子表示:①銷售該運動服每件的利潤是 ()元;②月銷量是 ()件;(直接寫出結果)
(2)設銷售該運動服的月利潤為y元,那么售價為多少時,當月的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】運用圖形變化的方法研究下列問題:如圖,AB是⊙O的直徑,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。則圖中陰影部分的面積是( )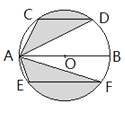
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為節約水資源,制定了新的居民用水收費標準.按照新標準,用戶每月繳納的水費y(元)與每月用水量x(m3)之間的關系如圖所示.
(1)求y關于x的函數解析式;
(2)若某用戶二、三月份共用水40m3(二月份用水量不超過25m3),繳納水費79.8元,則該用戶二、三月份的用水量各是多少m3?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將-1、![]() 、
、![]() 、2、
、2、![]() 、
、![]() ……按下面的規律排列,若規定(m,n)表示第m排從左至右的第n個數,那么表示(7,2)和(8,4)的數的積是____________.
……按下面的規律排列,若規定(m,n)表示第m排從左至右的第n個數,那么表示(7,2)和(8,4)的數的積是____________.
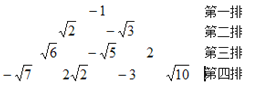
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com