
【題目】已知![]() 是
是![]() 的函數,自變量
的函數,自變量![]() 的取值范圍為
的取值范圍為![]() ,下表是
,下表是![]() 與
與![]() 的幾組對應值
的幾組對應值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根據學習函數的經驗,利用上述表格所反映出的![]() 與
與![]() 之間的變化規律,對該函數的圖象與性質進行了探究.下面是小明的探究過程,請補充完整:
之間的變化規律,對該函數的圖象與性質進行了探究.下面是小明的探究過程,請補充完整:
(1)如圖,在平面直角坐標系中,指出了以上表中各對對應值為坐標的點. 根據描出的點,畫出該函數的圖象.

(2)根據畫出的函數圖象填空.
①該函數圖象與![]() 軸的交點坐標為_____.
軸的交點坐標為_____.
②直接寫出該函數的一條性質.
【答案】(1)見解析;(2)①(5,0);②見解析.
【解析】
(1)根據坐標,連接點即可得出函數圖像;
(2)①根據圖像,當x≥3時,根據兩點坐標可得出函數解析式,進而可得出與![]() 軸的交點坐標;
軸的交點坐標;
②根據函數圖像,相應的自變量的取值范圍,可得出其性質.
(1) 如圖:
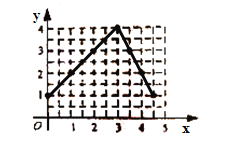
(2)①(5,0)
根據圖像,當x≥3時,函數圖像為一次函數,
設函數解析式為![]() ,將(3,4)和(4,2)兩點代入,即得
,將(3,4)和(4,2)兩點代入,即得
![]()
解得![]()
即函數解析式為![]()
與x軸的交點坐標為(5,0);
②答案不唯一.如下幾種答案供參考:
當0≤x≤3時,函數值y隨x值增大而增大;
當x≥3時,函數值y隨x值增大而減小;
當x=3時,函數有最大值為4;
該函數沒有最小值.


 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,O是坐標原點,長方形OACB的頂點A、B分別在x軸與y軸上,已知OA=6,OB=10.點D為y軸上一點,其坐標為(0,2),點P從點A出發以每秒2個單位的速度沿線段AC﹣CB的方向運動,當點P與點B重合時停止運動,運動時間為t秒.
(1)當點P經過點C時,求直線DP的函數解析式;
(2)①求△OPD的面積S關于t的函數解析式;
②如圖②,把長方形沿著OP折疊,點B的對應點B′恰好落在AC邊上,求點P的坐標.
(3)點P在運動過程中是否存在使△BDP為等腰三角形?若存在,請求出點P的坐標;若不存在,請說明理由.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師在黑板上書寫了一個正確的演算過程,隨后用手掌捂住了一個多項式,形式如下:
![]()
(1)求所捂的多項式;
(2)若x為正整數,任取x的幾個值并求出所捂多項式的值,你能發現什么規律?
(3)若所捂多項式的值為144,請直接寫出正整數x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知單位長度為1的方格中有三角形ABC.
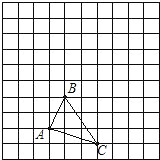
(1)請畫出三角形ABC向上平移3格再向右平移2格后所得到的三角形A′B′C′;
(2)請以點A為坐標原點建立平面直角坐標系(在圖中畫出),然后寫出點B,B′的坐標;
(3)求出三角形ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC是一張等腰直角三角形紙板,∠C=Rt∠,AC=BC=2,在這張紙板中剪出一個盡可能大的正方形稱為第1次剪取,記所得正方形面積為s1(如圖1);在余下的Rt△ADE和Rt△BDF中,分別剪取正方形,得到兩個相同的正方形,稱為第2次剪取,并記這兩個正方形面積和為s2(如圖2);繼續操作下去…;則第10次剪取時,s10= ;第2012次剪取后,余下的所有小三角形的面積之和是
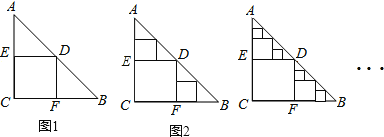
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)證明:無論m為何值方程都有兩個實數根;
(2)是否存在正數m,使方程的兩個實數根的平方和等于26?若存在,求出滿足條件的正數m的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)如圖是某種窗戶的形狀,其上部是半圓形,下部是邊長相同的四個小正方形,已知下部的小正方形的邊長為am,計算:
(1)窗戶的面積;
(2)窗框的總長;
(3)若a=1,窗戶上安裝的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不計,求制作這種窗戶需要的費用是多少元(π取3.14,結果保留整數).
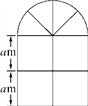
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,對于一個圖形,通過兩種不同的方法計算它的面積,可以得到一個數學等式.例如圖![]() 可以得到
可以得到![]()
![]() .請解答下列問題:
.請解答下列問題:

(1)寫出圖![]() 中所表示的數學等式;
中所表示的數學等式;

(2)利用(1)中所得到的結論,解決下面的問題:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同學打算用![]() 張邊長為
張邊長為![]() 的正方形,
的正方形,![]() 張邊長為
張邊長為![]() 的正方形,
的正方形,![]() 張相鄰兩邊長為分別為
張相鄰兩邊長為分別為![]() 、
、![]() 的長方形紙片拼出了一個面積為
的長方形紙片拼出了一個面積為 ![]() 長方形,那么他總共需要多少張紙片?
長方形,那么他總共需要多少張紙片?
查看答案和解析>>
科目:初中數學 來源: 題型:
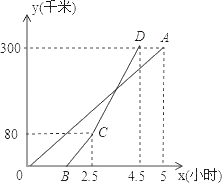
【題目】甲、乙兩地相距300千米,一輛貨車和一輛轎車先后從甲地出發向乙地,如圖,線段OA表示貨車離甲地距離y(千米)與時間x(小時)之間的函數關系;折線BCD表示轎車離甲地距離y(千米)與x(小時)之間的函數關系.請根據圖象解答下列問題:
(1)轎車到達乙地后,貨車距乙地多少千米?
(2)求線段CD對應的函數解析式.
(3)轎車到達乙地后,馬上沿原路以CD段速度返回,求貨車從甲地出發后多長時間再與轎車相遇(結果精確到0.01).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com