
【題目】如圖,在![]() 中,
中,![]() 點
點![]() 為直線
為直線![]() 上一點,點
上一點,點![]() 為
為![]() 延長線上一點,且
延長線上一點,且![]() ,連接
,連接![]() .
.
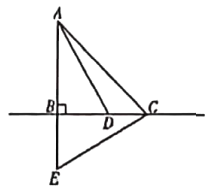
![]() 求證:
求證:![]() ;
;
![]() 當
當![]() 時,求
時,求![]() 的度數;
的度數;
![]() 點
點![]() 是
是![]() 的外心,當點
的外心,當點![]() 在直線
在直線![]() 上運動,且點
上運動,且點![]() 恰好在
恰好在![]() 內部或邊上時,直接寫出點
內部或邊上時,直接寫出點![]() 運動的路徑的長,
運動的路徑的長,
【答案】(1)見解析;(2):∠E=65°或25°;(3)![]()
【解析】
(1)(1)利用“邊角邊”證明即可;
(2)分兩種情況:點D在線段BC上時和點D在BC延長線上時,利用全等三角形對應角相等,推出∠E=∠ADB,再根據等腰直角三角形的性質求出∠ACB=∠CAB=45°,根據外角性質求出∠ADB,即可解答;
(3)過點B作BF垂直AC,交AC于F,作DC邊的垂直平分線交BF于點P,過點F作FG⊥BC,交BC于點G,證明BF是AC的垂直平分線,從而推出點P即為三角形CAD的外心,根據點![]() 恰好在
恰好在![]() 內部或邊上,確定點
內部或邊上,確定點![]() 運動的路徑為BF,求BF的長即可.
運動的路徑為BF,求BF的長即可.
(1)∵∠ABC=90°,
∴∠CBE=90°=∠ABC,
∵AB=CB, BE=BD,
∴ △ABD≌△CBE;
(2)當點D在線段BC上時,
∵△ABD≌△CBE,
∴∠E=∠ADB,
∵AB=CB,∠ABC=90°,
∴∠ACB=∠BAC=45°,
∴∠E=∠ADB=45°+20°=65°;
當點D在BC延長線上時,如圖,
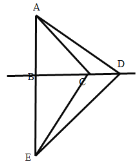
∵△ABD≌△CBE,
∴∠BEC=∠ADB,
∵AB=CB,∠ABC=90°,
∴∠ACB=∠BAC=45°,
∴∠BEC=∠ADB=45°-20°=25°;
綜上:∠E=65°或25°.
(3)如圖,過點B作BF垂直AC,交AC于F,作DC邊的垂直平分線交BF于點P,過點F作FG⊥BC,交BC于點G,
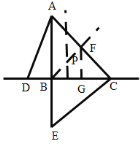
∵![]() BF⊥AC,
BF⊥AC,
∴BF是AC的垂直平分線,
∴點P即為三角形CAD的外心.
∵P為BF上一點,
由題意可知點![]() 恰好在
恰好在![]() 內部或邊上,
內部或邊上,
∴點![]() 運動的路徑為BF,
運動的路徑為BF,
∵![]()
∴![]() ,
,
∵BF是AC的垂直平分線,
∴BF=![]() ,
,
即點P的運動路徑長為![]()


科目:初中數學 來源: 題型:
【題目】如圖,已知正比例函數和反比例函數的圖像都經過點![]() ,且
,且![]() 為雙曲線上的一點,
為雙曲線上的一點,![]() 為坐標平面上一動點,
為坐標平面上一動點,![]() 垂直于
垂直于![]() 軸,
軸,![]() 垂直于
垂直于![]() 軸,垂足分別是
軸,垂足分別是![]() 、
、![]() .
.
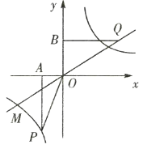
(1)寫出正比例函數和反比例函數的關系式.
(2)當點![]() 在直線
在直線![]() 上運動時,直線
上運動時,直線![]() 上是否存在這樣的點
上是否存在這樣的點![]() ,使得
,使得![]() 與
與![]() 的面積相等?如果存在,請求出點的坐標;如果不存在,請說明理由.
的面積相等?如果存在,請求出點的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC=4![]() ,∠C=90°,點D在BC上,且CD=3DB,將△ABC折疊,使點A與點D重合,EF為折痕,則tan∠BED的值是_____.
,∠C=90°,點D在BC上,且CD=3DB,將△ABC折疊,使點A與點D重合,EF為折痕,則tan∠BED的值是_____.
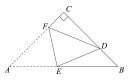
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某科普小組有5名成員,身高(單位:cm)分別為:160,165,170,163,172,把身高160 cm的成員替換成一位165 cm的成員后,現科普小組成員的身高與原來相比,下列說法正確的是( )
A.平均數變小,方差變小B.平均數變大,方差變大
C.平均數變大,方差不變D.平均數變大,方差變小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】同型號的甲、乙兩輛車加滿氣體燃料后均可行駛210km.它們各自單獨行駛并返回的最遠距離是105km.現在它們都從A地出發,行駛途中停下來從甲車的氣體燃料桶抽一些氣體燃料注入乙車的氣體燃料桶,然后甲車再行駛返回A地,而乙車繼續行駛,到B地后再行駛返回A地.則B地最遠可距離A地( )
A.120kmB.140kmC.160kmD.180km
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:如圖,在△ABD中,BA=BD.在BD的延長線上取點E,C,作△AEC,使EA=EC,若∠BAE=90°,∠B=45°,求∠DAC的度數.
答案:∠DAC=45°
思考:(1)如果把以上“問題”中的條件“∠B=45°”去掉,其余條件不變,那么∠DAC的度數會改變嗎?說明理由;
(2)如果把以上“問題”中的條件“∠B=45°”去掉,再將“∠BAE=90°”改為“∠BAE=n°”,其余條件不變,求∠DAC的度數.
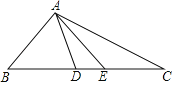
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車經營店銷售![]() 型,
型,![]() 型兩種品牌自行車,今年進貨和銷售價格如下表:(今年1年內自行車的售價與進價保持不變)
型兩種品牌自行車,今年進貨和銷售價格如下表:(今年1年內自行車的售價與進價保持不變)
|
| |
進貨價格(元/輛) | 1000 | 1100 |
銷售價格(元/輛) |
| 1500 |
今年經過改造升級后,![]() 型車每輛銷售價比去年增加400元.已知
型車每輛銷售價比去年增加400元.已知![]() 型車去年1月份銷售總額為3.6萬元,今年1月份
型車去年1月份銷售總額為3.6萬元,今年1月份![]() 型車的銷售數量與去年1月份相同,而銷售總額比去年1月份增加
型車的銷售數量與去年1月份相同,而銷售總額比去年1月份增加![]() .
.
(1)若設今年1月份的![]() 型自行車售價為
型自行車售價為![]() 元/輛,求
元/輛,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)該店計劃8月份再進一批![]() 型和
型和![]() 型自行車共50輛,且
型自行車共50輛,且![]() 型車數量不超過
型車數量不超過![]() 型車數量的2倍,應如何進貨才能使這批自行車獲利最多?
型車數量的2倍,應如何進貨才能使這批自行車獲利最多?
(3)該店為吸引客源,準備增購一種進價為500元的![]() 型車,預算用8萬元購進這三種車若干輛,其中
型車,預算用8萬元購進這三種車若干輛,其中![]() 型與
型與![]() 型的數量之比為
型的數量之比為![]() ,則該店至少可以購進三種車共多少輛?
,則該店至少可以購進三種車共多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著科技的進步和網絡資源的豐富,在線學習已成為更多人的自主學習選擇.某校計劃為學生提供以下四類在線學習方式:在線閱讀、在線聽課、在線答題和在線討論.為了解學生需求,該校隨機對本校部分學生進行了“你對哪類在線學習方式最感興趣”的調查,并根據調查結果繪制成如下兩幅不完整的統計圖.
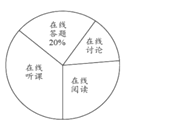
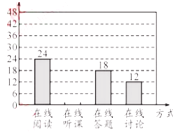
根據圖中信息,解答下列問題:
(1)求本次調查的學生總人數,并補全條形統計圖;
(2)求扇形統計圖中“在線討論”對應的扇形圓心角的度數;
(3)該校共有學生![]() 人,請你估計該校對在線閱讀最感興趣的學生人數.
人,請你估計該校對在線閱讀最感興趣的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com